
بهینهسازی بیزی (BayesOpt) ابزار قدرتمندی است که به طور گسترده برای کارهای بهینهسازی جهانی، مانند تنظیم فراپارامتر، مهندسی پروتئین، شیمی مصنوعی، یادگیری ربات و حتی پخت کوکیها استفاده میشود. BayesOpt یک استراتژی عالی برای این مشکلات است زیرا همه آنها شامل بهینه سازی توابع جعبه سیاه هستند که ارزیابی آنها پرهزینه است. نقشهبرداری اساسی تابع جعبه سیاه از ورودیها (پیکربندیهای چیزی که میخواهیم بهینهسازی کنیم) تا خروجیها (معیار عملکرد) ناشناخته است. با این حال، ما میتوانیم با ارزیابی تابع برای ترکیبهای مختلف ورودیها، عملکرد داخلی آن را درک کنیم. از آنجا که هر ارزیابی می تواند از نظر محاسباتی گران باشد، ما باید بهترین ورودی ها را در کمترین ارزیابی ممکن پیدا کنیم. BayesOpt با ساخت مکرر یک مدل جایگزین از تابع جعبه سیاه و ارزیابی استراتژیک عملکرد در امیدوار کننده ترین یا آموزنده ترین مکان ورودی، با توجه به اطلاعات مشاهده شده تاکنون، کار می کند.
فرآیندهای گاوسی مدلهای جایگزین محبوب برای BayesOpt هستند، زیرا استفاده از آنها آسان است، میتوان آنها را با دادههای جدید بهروزرسانی کرد و سطح اطمینانی را در مورد هر یک از پیشبینیهای آنها ارائه میکند. مدل فرآیند گاوسی توزیع احتمال را بر روی توابع ممکن می سازد. این توزیع با یک تابع میانگین (این توابع ممکن به طور متوسط چگونه به نظر می رسند) و یک تابع هسته (این توابع چقدر می توانند در ورودی ها متفاوت باشند) مشخص می شود. عملکرد BayesOpt به این بستگی دارد که آیا فواصل اطمینان پیش بینی شده توسط مدل جایگزین شامل تابع جعبه سیاه است یا خیر. به طور سنتی، کارشناسان از دانش دامنه برای تعریف کمی پارامترهای میانگین و هسته (به عنوان مثال، محدوده یا صاف بودن تابع جعبه سیاه) استفاده می کنند تا انتظارات خود را در مورد اینکه تابع جعبه سیاه چگونه باید باشد، بیان کنند. با این حال، برای بسیاری از کاربردهای دنیای واقعی مانند تنظیم فراپارامتر، درک مناظر اهداف تنظیم بسیار دشوار است. حتی برای کارشناسان با تجربه مرتبط، محدود کردن پارامترهای مدل مناسب میتواند چالش برانگیز باشد.
در «فرایندهای گوسی از پیش آموزشدیده برای بهینهسازی بیزی»، چالش بهینهسازی فراپارامتر برای شبکههای عصبی عمیق با استفاده از BayesOpt را در نظر میگیریم. ما Hyper BayesOpt (HyperBO) را پیشنهاد می کنیم، یک رابط بسیار قابل تنظیم با الگوریتمی که نیاز به کمی کردن پارامترهای مدل برای فرآیندهای گاوسی در BayesOpt را حذف می کند. برای مسائل بهینهسازی جدید، کارشناسان میتوانند به سادگی وظایف قبلی را انتخاب کنند که مربوط به کار فعلی است که سعی در حل آن دارند. HyperBO یک مدل فرآیند گاوسی را بر روی داده های آن وظایف انتخاب شده از قبل آموزش می دهد و به طور خودکار پارامترهای مدل را قبل از اجرای BayesOpt تعریف می کند. HyperBO از ضمانتهای نظری در مورد همسویی بین مدل از پیش آموزشدیده و حقیقت زمین و همچنین کیفیت راهحلهای خود برای بهینهسازی جعبه سیاه برخوردار است. ما نتایج قوی HyperBO را در معیارهای تنظیم جدید خود برای مدلهای یادگیری عمیق تقریباً پیشرفته و معیارهای بهینهسازی جعبه سیاه چند کاره کلاسیک (HPO-B) به اشتراک میگذاریم. ما همچنین نشان میدهیم که HyperBO در انتخاب وظایف مربوطه قوی است و نیازهای کمی در میزان دادهها و وظایف برای پیشآموزش دارد.
 |
| در رابط سنتی BayesOpt، کارشناسان باید پارامترهای میانگین و هسته را برای یک مدل فرآیند گاوسی با دقت انتخاب کنند. HyperBO این مشخصات دستی را با مجموعه ای از وظایف مرتبط جایگزین می کند و استفاده از بهینه سازی بیزی را آسان تر می کند. وظایف انتخاب شده برای پیشآموزش مورد استفاده قرار میگیرند، جایی که ما یک فرآیند گاوسی را بهینه میکنیم تا بتواند به تدریج توابعی را ایجاد کند که مشابه توابع مربوط به آن وظایف انتخاب شده است. شباهت در مقادیر تک تک تابع و تغییرات مقادیر تابع در ورودی ها آشکار می شود. |
توابع از دست دادن برای قبل از آموزش
ما یک مدل فرآیند گاوسی را با به حداقل رساندن واگرایی Kullback-Leibler (یک واگرایی رایج) بین مدل حقیقت زمینی و مدل از پیش آموزشدیده شده، از قبل آموزش میدهیم. از آنجایی که مدل حقیقت زمینی ناشناخته است، نمیتوانیم مستقیماً این تابع از دست دادن را محاسبه کنیم. برای حل این موضوع، ما دو تقریب مبتنی بر داده را معرفی میکنیم: (1) واگرایی تجربی کولبک-لایبلر (EKL)، که واگرایی بین تخمین تجربی مدل حقیقت زمینی و مدل از پیش آموزشدیده است. (2) احتمال ورود به سیستم منفی (NLL)، که مجموع احتمالات ورود به سیستم منفی مدل از پیش آموزش دیده برای همه توابع آموزشی است. هزینه محاسباتی EKL یا NLL به صورت خطی با تعداد توابع آموزشی مقیاس می شود. علاوه بر این، روشهای مبتنی بر گرادیان تصادفی مانند Adam میتوانند برای بهینهسازی توابع از دست دادن استفاده شوند، که هزینه محاسبات را بیشتر کاهش میدهد. در محیط های به خوبی کنترل شده، بهینه سازی EKL و NLL منجر به یک نتیجه می شود، اما چشم اندازهای بهینه سازی آنها می تواند بسیار متفاوت باشد. برای مثال، در سادهترین حالت که تابع فقط یک ورودی ممکن دارد، مدل فرآیند گاوسی آن به یک توزیع گاوسی تبدیل میشود که با میانگین توصیف میشود (متر) و واریانس (س). بنابراین تابع ضرر فقط آن دو پارامتر را دارد، متر و س، و می توانیم EKL و NLL را به صورت زیر تجسم کنیم:
 |
| ما مناظر از دست دادن EKL را شبیه سازی می کنیم (ترک کرد) و NLL (درست) برای یک مدل ساده با پارامترها متر و س. رنگ ها نشان دهنده یک نقشه حرارتی از مقادیر EKL یا NLL هستند، که در آن قرمز مربوط به مقادیر بالاتر و آبی نشان دهنده مقادیر پایین تر است. این دو چشم انداز از دست دادن بسیار متفاوت هستند، اما هر دو هدف آن ها تطبیق مدل از پیش آموزش دیده با مدل حقیقت زمینی هستند. |
پیش تمرین بهینه سازی بیزی را بهبود می بخشد
در الگوریتم BayesOpt، تصمیم گیری در مورد محل ارزیابی تابع جعبه سیاه به صورت مکرر اتخاذ می شود. معیارهای تصمیم گیری بر اساس سطوح اطمینان ارائه شده توسط فرآیند گاوسی است که در هر تکرار با شرطی کردن نقاط داده قبلی به دست آمده توسط BayesOpt به روز می شود. به طور شهودی، سطوح اطمینان به روز شده باید درست باشد: نه بیش از حد مطمئن یا خیلی نامطمئن، زیرا در هر یک از این دو مورد، BayesOpt نمی تواند تصمیماتی را اتخاذ کند که می تواند مطابق با کاری باشد که یک متخصص انجام می دهد.
در HyperBO، مدل دستی را در BayesOpt سنتی با فرآیند گاوسی از پیش آموزشدیده جایگزین میکنیم. تحت شرایط ملایم و با توابع آموزشی کافی، میتوانیم از نظر ریاضی ویژگیهای نظری خوب HyperBO را تأیید کنیم: (1) تراز: فرآیند گاوسی از پیش آموزشدیده شده تضمین میکند که به مدل حقیقت زمین نزدیک باشد، زمانی که هر دو بر اساس نقاط داده مشاهدهشده مشروط شوند. (2) بهینه: HyperBO تضمین می کند که یک راه حل تقریباً بهینه برای مسئله بهینه سازی جعبه سیاه برای هر توابعی که بر اساس فرآیند ناشناخته حقیقت زمینی گاوسی توزیع شده است پیدا کند.
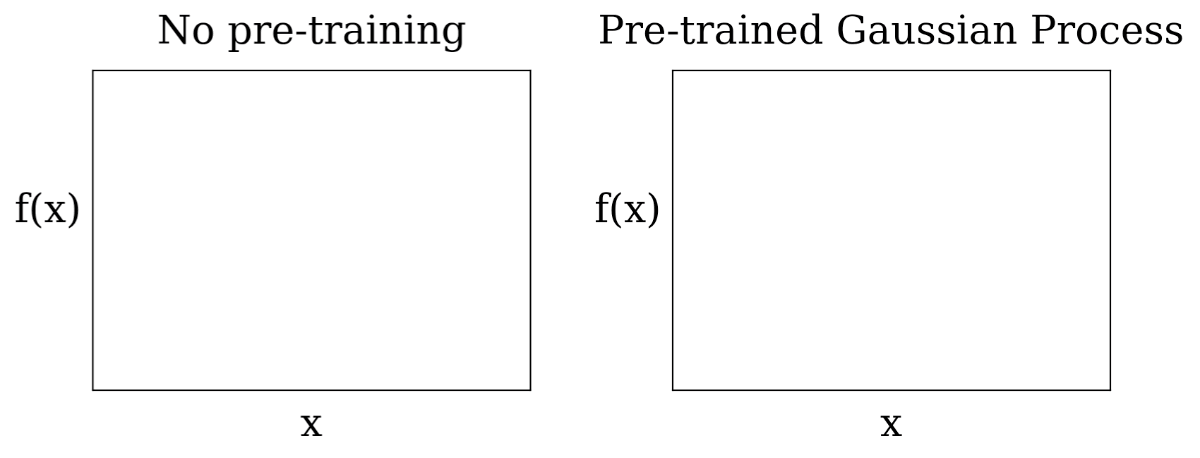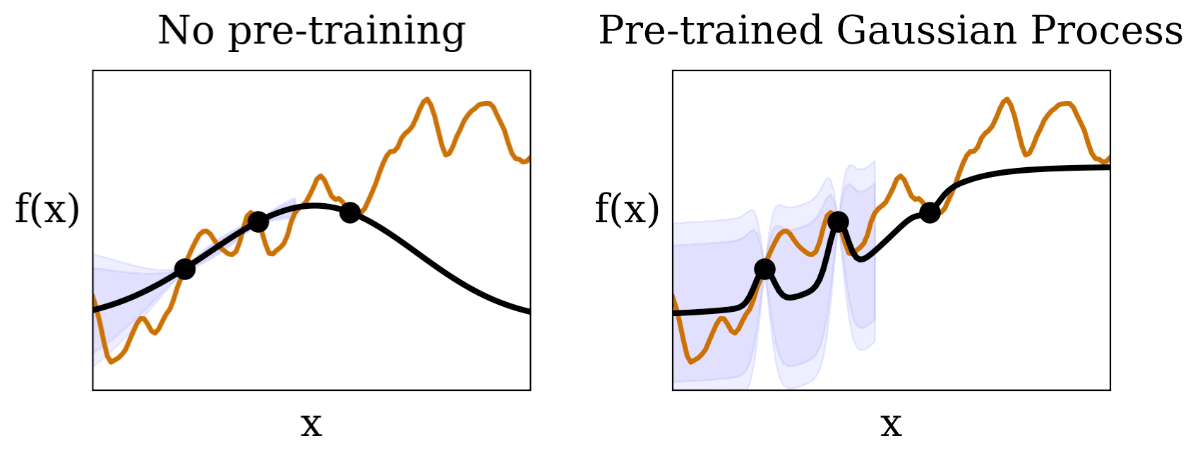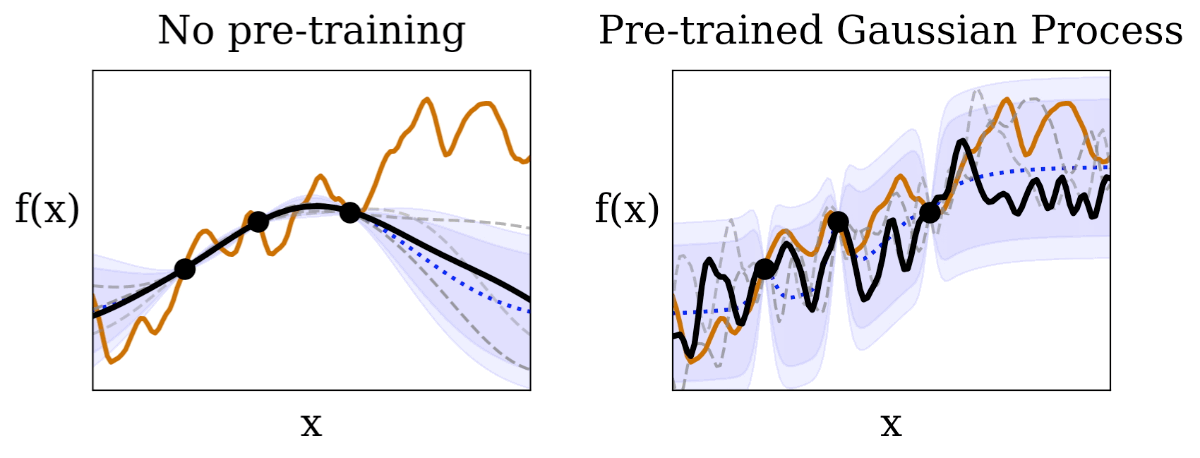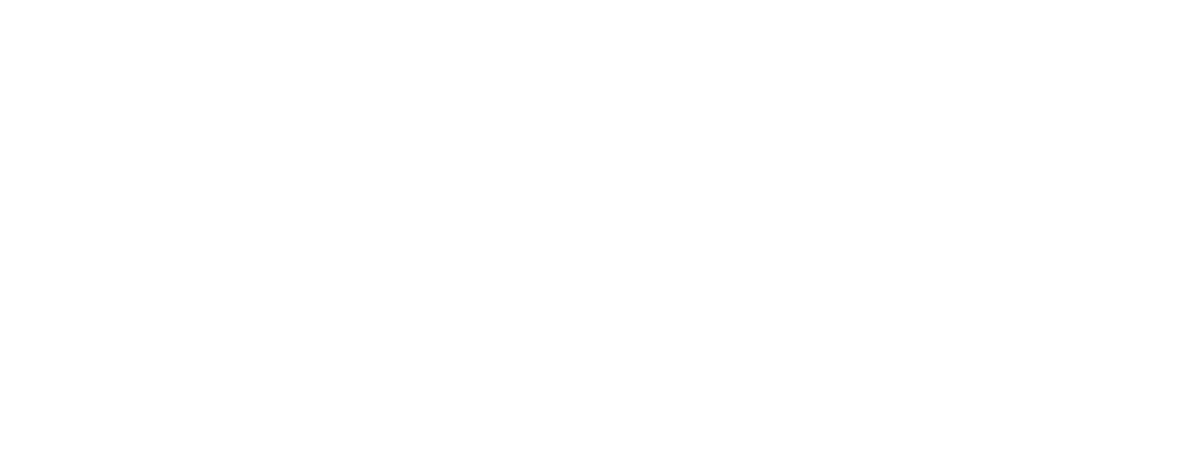 |
| ما فرآیند گاوسی را تجسم می کنیم (مناطق با رنگ بنفش 95٪ و 99٪ فواصل اطمینان هستند) مشروط به مشاهدات (نقاط سیاه) از یک تابع آزمایشی ناشناخته (خط نارنجی). در مقایسه با BayesOpt سنتی بدون پیشآموزش، سطوح اطمینان پیشبینیشده در HyperBO عملکرد تست ناشناخته را بسیار بهتر نشان میدهد، که یک پیشنیاز حیاتی برای بهینهسازی بیزی است. |
از نظر تجربی، برای تعریف ساختار فرآیندهای گاوسی از قبل آموزشدیده، ما انتخاب میکنیم که از توابع میانگین بسیار گویا مدلسازی شده توسط شبکههای عصبی استفاده کنیم و توابع هسته به خوبی تعریف شده را بر روی ورودیهای کدگذاری شده در فضای ابعاد بالاتر با شبکههای عصبی اعمال کنیم.
برای ارزیابی HyperBO در مسائل چالش برانگیز و واقعی بهینه سازی جعبه سیاه، ما معیار PD1 را ایجاد کردیم که شامل مجموعه داده ای برای بهینه سازی هایپرپارامتر چند وظیفه ای برای شبکه های عصبی عمیق است. PD1 با آموزش دهها هزار پیکربندی از مدلهای یادگیری عمیق تقریباً پیشرفته بر روی مجموعه دادههای تصویری و متنی محبوب و همچنین مجموعه دادههای توالی پروتئین توسعه داده شد. PD1 شامل تقریباً 50000 ارزیابی هایپرپارامتر از 24 کار مختلف (به عنوان مثال تنظیم Wide ResNet در CIFAR100) با تقریباً 12000 روز ماشین محاسبه می شود.
ما نشان میدهیم که هنگام پیشآموزش تنها برای چند ساعت روی یک CPU، HyperBO میتواند به طور قابلتوجهی از BayesOpt با مدلهایی که به دقت تنظیم شدهاند در کارهای چالشبرانگیز دیده نشده، از جمله تنظیم ResNet50 در ImageNet، بهتر عمل کند. حتی با وجود تنها 100 نقطه داده در هر تابع آموزشی، HyperBO می تواند به صورت رقابتی در برابر خطوط پایه عمل کند.
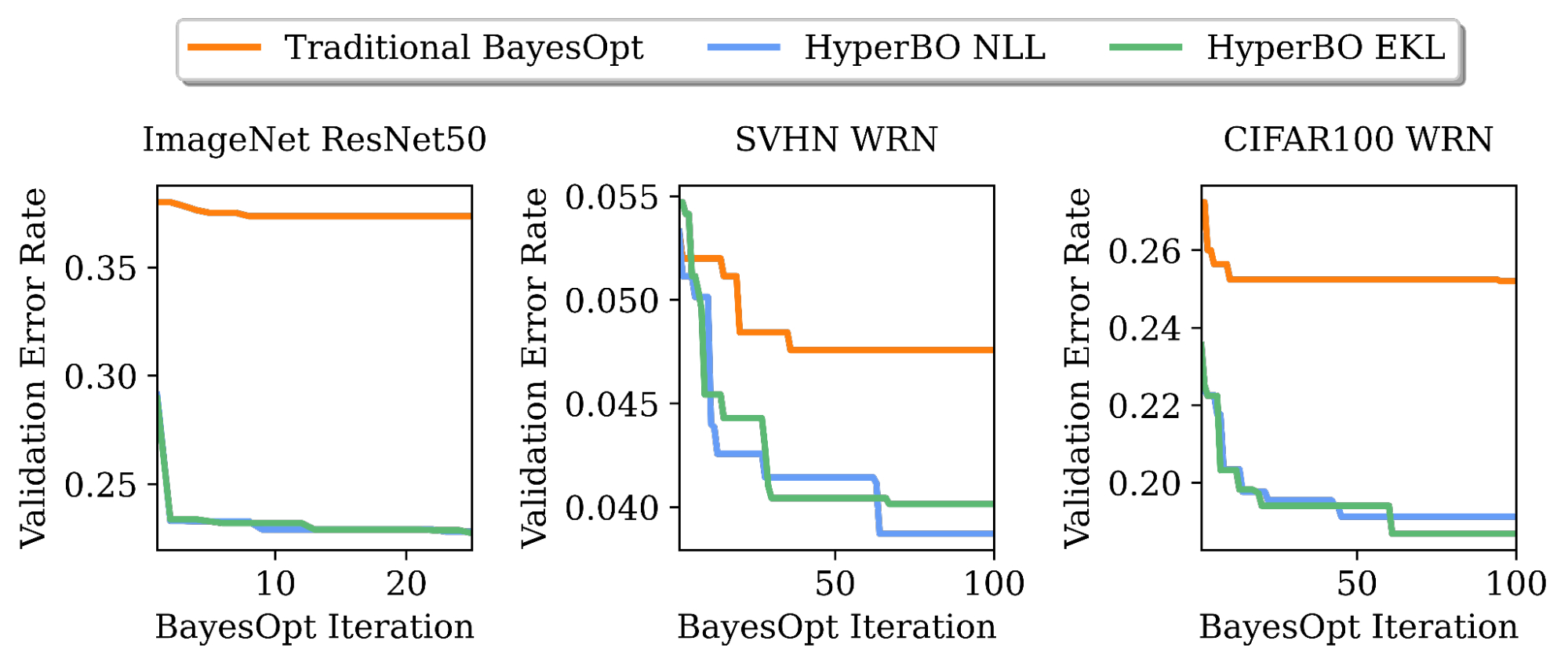 |
| تنظیم نرخ خطای اعتبارسنجی ResNet50 در ImageNet و Wide ResNet (WRN) در مجموعه داده Street View House Numbers (SVHN) و CIFAR100. HyperBO با پیشآموزش تنها بر روی 20 کار و 100 نقطه داده در هر کار، میتواند به طور قابلتوجهی بهتر از BayesOpt سنتی (با یک فرآیند گاوسی به دقت تنظیم شده) در کارهایی که قبلاً دیده نشده بود، پیشی بگیرد. |
نتیجه گیری و کار آینده
HyperBO چارچوبی است که یک فرآیند گاوسی را از قبل آموزش می دهد و متعاقباً بهینه سازی بیزی را با یک مدل از پیش آموزش دیده انجام می دهد. با HyperBO، دیگر لازم نیست پارامترهای کمی دقیق را در یک فرآیند گاوسی به صورت دستی مشخص کنیم. در عوض، ما فقط باید وظایف مرتبط و داده های مربوط به آنها را برای قبل از آموزش شناسایی کنیم. این باعث می شود BayesOpt هم در دسترس تر و هم موثرتر باشد. یک جهت مهم در آینده، فعال کردن HyperBO برای تعمیم فضاهای جستجوی ناهمگن است، که ما در حال توسعه الگوریتمهای جدید با پیش آموزش یک مدل احتمالی سلسله مراتبی هستیم.
سپاسگزاریها
اعضای زیر تیم تحقیقاتی مغز گوگل این تحقیق را انجام دادند: زی وانگ، جورج ای دال، کوین سورسکی، چانسو لی، زاکاری نادو، جاستین گیلمر، جاسپر اسنوک و زوبین قهرمانی. مایلیم از زلدا ماریت و ماتیاس فیورر برای کمک و مشاوره در زمینه مبانی یادگیری انتقال تشکر کنیم. ما همچنین میخواهیم از Rif A. Saurous برای بازخورد سازنده و Rodolphe Jenatton و David Belanger برای بازخورد در مورد نسخههای قبلی دستنوشته تشکر کنیم. علاوه بر این، از شرات چیکرور، بن آدلم، بالاجی لاکشمینارایانان، فی شا و ایتان بخشی برای نظرات و ستاره آریافر و الکساندر ترنین برای گفتگو در مورد انیمیشن تشکر می کنیم. در پایان از تام اسمال برای طراحی انیمیشن این پست تشکر می کنیم.