
شبکه های عصبی مدرن در کاربردهای مختلف مانند زبان، استدلال ریاضی و بینایی به عملکرد چشمگیری دست یافته اند. با این حال، این شبکه ها اغلب از معماری های بزرگی استفاده می کنند که به منابع محاسباتی زیادی نیاز دارند. این میتواند ارائه چنین مدلهایی به کاربران را غیرعملی کند، بهویژه در محیطهای با محدودیت منابع مانند پوشیدنیها و گوشیهای هوشمند. یک رویکرد پرکاربرد برای کاهش هزینههای استنتاج شبکههای از پیش آموزشدیده، هرس کردن آنها با حذف برخی از وزنهای آنها است، بهگونهای که تاثیر قابلتوجهی بر کاربرد ندارد. در شبکه های عصبی استاندارد، هر وزن ارتباط بین دو نورون را تعریف می کند. بنابراین پس از هرس وزنه ها، ورودی از طریق مجموعه کوچکتری از اتصالات منتشر می شود و بنابراین به منابع محاسباتی کمتری نیاز دارد.
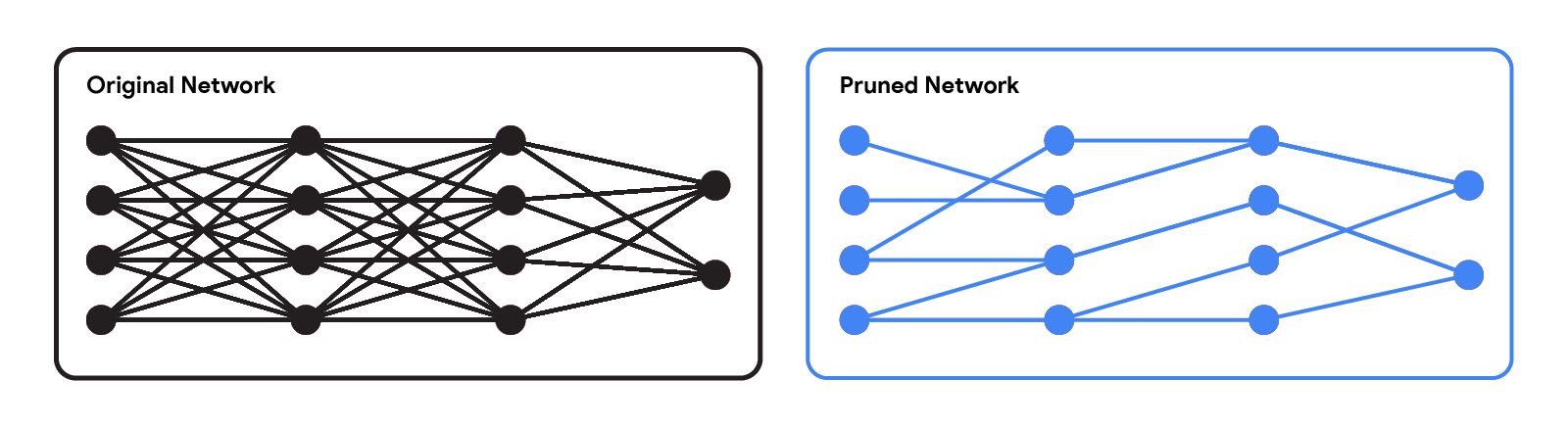 |
| شبکه اصلی در مقابل شبکه هرس شده. |
روشهای هرس را میتوان در مراحل مختلف فرآیند تمرین شبکه اعمال کرد: پس از تمرین، در حین یا قبل از تمرین (یعنی بلافاصله پس از تنظیم وزن). در این پست، ما بر روی تنظیمات پس از آموزش تمرکز می کنیم: با توجه به یک شبکه از قبل آموزش دیده، چگونه می توانیم تعیین کنیم که کدام وزنه ها باید هرس شوند؟ یکی از روشهای رایج هرس بزرگی است که وزنهایی را با کمترین بزرگی حذف میکند. اگرچه این روش کارآمد است، اما به طور مستقیم تأثیر حذف وزن ها بر عملکرد شبکه را در نظر نمی گیرد. پارادایم محبوب دیگر هرس مبتنی بر بهینه سازی است که وزن ها را بر اساس میزان تأثیر حذف آنها بر عملکرد از دست دادن حذف می کند. اگرچه از نظر مفهومی جذاب است، اما به نظر میرسد اکثر رویکردهای مبتنی بر بهینهسازی موجود با یک مبادله جدی بین عملکرد و الزامات محاسباتی روبرو هستند. روشهایی که تقریبهای خام میکنند (مثلاً با فرض یک ماتریس هسی مورب) میتوانند به خوبی مقیاس شوند، اما عملکرد نسبتاً پایینی دارند. از سوی دیگر، در حالی که روشهایی که تقریبهای کمتری انجام میدهند، عملکرد بهتری دارند، اما به نظر میرسد که مقیاسپذیری کمتری دارند.
در “سریع به عنوان CHITA: هرس شبکه عصبی با بهینه سازی ترکیبی”، ارائه شده در ICML 2023، ما توضیح می دهیم که چگونه یک رویکرد مبتنی بر بهینه سازی را برای هرس شبکه های عصبی از پیش آموزش دیده در مقیاس توسعه داده ایم. CHITA (که مخفف “Combinatorial Hessian-free Iterative Thresholding Algorithm” است) از روشهای هرس موجود از نظر مقیاسپذیری و معاوضه عملکرد بهتر عمل میکند و این کار را با استفاده از پیشرفتها از چندین زمینه، از جمله آمار با ابعاد بالا، بهینهسازی ترکیبی، و شبکه عصبی انجام میدهد. هرس کردن به عنوان مثال، CHITA می تواند 20 برابر تا 1000 برابر سریعتر از روش های پیشرفته برای هرس ResNet باشد و دقت را در بسیاری از تنظیمات بیش از 10٪ بهبود می بخشد.
مروری بر مشارکت ها
CHITA دو پیشرفت فنی قابل توجه نسبت به روش های رایج دارد:
- استفاده کارآمد از اطلاعات مرتبه دوم: روشهای هرس که از اطلاعات مرتبه دوم (یعنی مربوط به مشتقات دوم) استفاده میکنند، در بسیاری از موقعیتها به بهترین حالت دست مییابند. در ادبیات، این اطلاعات معمولاً با محاسبه ماتریس Hessian یا معکوس آن استفاده میشود، عملیاتی که مقیاسگذاری آن بسیار دشوار است، زیرا اندازه Hessian نسبت به تعداد وزنها درجه دوم است. از طریق فرمولبندی دقیق، CHITA از اطلاعات مرتبه دوم بدون نیاز به محاسبه یا ذخیره ماتریس Hessian به طور صریح استفاده میکند، بنابراین امکان مقیاسپذیری بیشتر را فراهم میکند.
- بهینه سازی ترکیبی: روشهای رایج مبتنی بر بهینهسازی از یک تکنیک بهینهسازی ساده استفاده میکنند که وزنها را بهصورت مجزا هرس میکند، بهعنوان مثال، هنگام تصمیمگیری برای هرس یک وزن خاص، در نظر نمیگیرند که آیا وزنهای دیگر هرس شدهاند یا خیر. این میتواند منجر به هرس وزنههای مهم شود، زیرا وزنههایی که بهطور مجزا بیاهمیت تلقی میشوند ممکن است زمانی که وزنههای دیگر هرس میشوند، مهم شوند. CHITA با استفاده از یک الگوریتم بهینهسازی ترکیبی پیشرفتهتر از این موضوع جلوگیری میکند که در نظر گرفتن این که چگونه هرس یک وزنه روی وزنهها تأثیر میگذارد.
در بخش های زیر، فرمول و الگوریتم های هرس CHITA را مورد بحث قرار می دهیم.
یک فرمول هرس محاسباتی
نامزدهای احتمالی زیادی برای هرس وجود دارد که تنها با حفظ زیر مجموعه ای از وزن ها از شبکه اصلی به دست می آیند. اجازه دهید ک یک پارامتر مشخص شده توسط کاربر باشد که تعداد وزن هایی را که باید حفظ شود را نشان می دهد. هرس را می توان به طور طبیعی به عنوان یک مسئله انتخاب بهترین زیر مجموعه (BSS) فرموله کرد: در بین همه نامزدهای هرس ممکن (یعنی زیر مجموعه وزن ها) فقط با ک با حفظ وزن، کاندیدایی که کمترین کاهش را داشته باشد انتخاب می شود.
 |
| هرس به عنوان یک مشکل BSS: در بین همه نامزدهای احتمالی هرس با تعداد کل وزنهای یکسان، بهترین نامزد به عنوان یکی با کمترین ضرر تعریف میشود. این تصویر چهار نامزد را نشان می دهد، اما این تعداد به طور کلی بسیار بزرگتر است. |
حل مسئله هرس BSS در تابع ضرر اصلی معمولاً از نظر محاسباتی غیرقابل حل است. بنابراین، مشابه کارهای قبلی، مانند OBD و OBS، با استفاده از یک سری تیلور مرتبه دوم، تلفات را با یک تابع درجه دوم تقریب میکنیم، که در آن هسین با ماتریس اطلاعات تجربی فیشر تخمین زده میشود. در حالی که گرادیان ها را می توان به طور معمول به طور موثر محاسبه کرد، محاسبه و ذخیره ماتریس Hessian به دلیل اندازه بزرگ آن بسیار گران است. در ادبیات، مقابله با این چالش با ایجاد مفروضات محدود کننده بر روی Hessian (به عنوان مثال، ماتریس مورب) و همچنین در الگوریتم (به عنوان مثال، هرس وزن ها به صورت مجزا) معمول است.
CHITA از فرمول بندی مجدد کارآمد مسئله هرس (BSS با استفاده از تلفات درجه دوم) استفاده می کند که از محاسبه صریح ماتریس Hessian اجتناب می کند، در حالی که هنوز از تمام اطلاعات این ماتریس استفاده می کند. این امر با بهره برداری از ساختار پایین رتبه ماتریس اطلاعات تجربی فیشر امکان پذیر شده است. این فرمول بندی مجدد را می توان به عنوان یک مسئله رگرسیون خطی پراکنده مشاهده کرد، که در آن هر ضریب رگرسیون مربوط به وزن خاصی در شبکه عصبی است. پس از به دست آوردن یک راه حل برای این مشکل رگرسیون، ضرایب تنظیم شده بر روی صفر مطابق با وزن هایی است که باید هرس شوند. ماتریس داده های رگرسیون ما (n ایکس پ)، جایی که n اندازه دسته ای (نمونه فرعی) و پ تعداد وزن ها در شبکه اصلی است. معمولا n << پبنابراین ذخیره سازی و عملکرد با این ماتریس داده بسیار مقیاس پذیرتر از روش های هرس معمولی است که با (پ ایکس پ) حصیر.
 |
| CHITA تقریب تلفات درجه دوم را که به یک ماتریس هسین گران قیمت نیاز دارد، به عنوان یک مسئله رگرسیون خطی (LR) فرموله می کند. ماتریس داده LR خطی است پ، که فرمول بندی مجدد را نسبت به تقریب درجه دوم مقیاس پذیرتر می کند. |
الگوریتم های بهینه سازی مقیاس پذیر
CHITA هرس را به یک مشکل رگرسیون خطی تحت محدودیت پراکندگی زیر کاهش می دهد: حداکثر: ک ضرایب رگرسیون می تواند غیر صفر باشد. برای به دست آوردن راه حلی برای این مشکل، اصلاحی از الگوریتم شناخته شده آستانه سخت تکراری (IHT) را در نظر می گیریم. IHT نزول گرادیان را انجام می دهد که در آن پس از هر به روز رسانی مرحله پس پردازش زیر انجام می شود: همه ضرایب رگرسیون خارج از Top-ک (یعنی ک ضرایب با بزرگترین قدر) روی صفر تنظیم می شوند. IHT معمولاً یک راه حل خوب برای مشکل ارائه می دهد و این کار را به طور مکرر با بررسی نامزدهای مختلف هرس و بهینه سازی مشترک روی وزن ها انجام می دهد.
با توجه به مقیاس مشکل، IHT استاندارد با نرخ یادگیری ثابت می تواند از همگرایی بسیار کند رنج ببرد. برای همگرایی سریعتر، ما یک روش جستجوی خطی جدید ایجاد کردیم که از ساختار مسئله برای یافتن نرخ یادگیری مناسب استفاده میکند، یعنی نرخی که منجر به کاهش به اندازه کافی بزرگ در ضرر شود. ما همچنین از چندین طرح محاسباتی برای بهبود کارایی CHITA و کیفیت تقریب مرتبه دوم استفاده کردیم که منجر به نسخه بهبود یافتهای شد که آن را CHITA++ مینامیم.
آزمایش
ما زمان اجرا و دقت CHITA را با چندین روش هرس پیشرفته با استفاده از معماریهای مختلف از جمله ResNet و MobileNet مقایسه میکنیم.
زمان اجرا: CHITA بسیار مقیاس پذیرتر از روش های مقایسه ای است که بهینه سازی مشترک را انجام می دهند (برخلاف وزنه های هرس به صورت مجزا). به عنوان مثال، سرعت CHITA می تواند به بیش از 1000 برابر در هنگام هرس ResNet برسد.
دقت پس از هرس: در زیر، ما عملکرد CHITA و CHITA++ را با هرس بزرگی (MP)، Woodfisher (WF) و Combinatorial Brain Surgeon (CBS) برای هرس کردن 70 درصد وزنهای مدل مقایسه میکنیم. به طور کلی، شاهد پیشرفت های خوبی از CHITA و CHITA++ هستیم.
 |
| دقت پس از هرس روش های مختلف در ResNet20. نتایج برای هرس 70 درصد از وزن مدل گزارش شده است. |
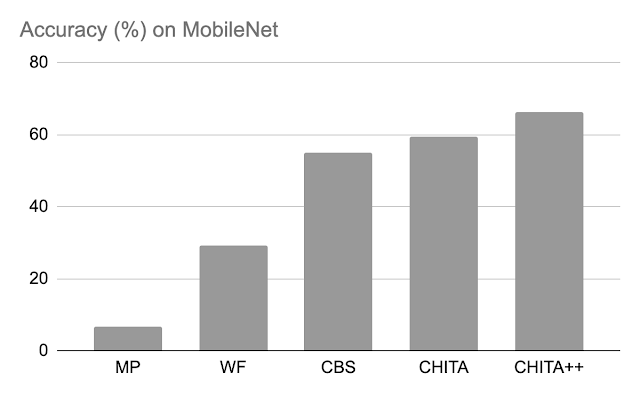 |
| دقت پس از هرس روش های مختلف در موبایل نت. نتایج برای هرس 70 درصد از وزن مدل گزارش شده است. |
سپس، نتایج را برای هرس کردن یک شبکه بزرگتر گزارش میکنیم: ResNet50 (در این شبکه، برخی از روشهای فهرستشده در شکل ResNet20 نمیتوانند مقیاس شوند). در اینجا ما با هرس بزرگی و M-FAC مقایسه می کنیم. شکل زیر نشان می دهد که CHITA به دقت تست بهتری برای طیف وسیعی از سطوح پراکندگی دست می یابد.
 |
| دقت تست شبکه های هرس شده با استفاده از روش های مختلف به دست آمده است. |
نتیجه گیری، محدودیت ها، و کار آینده
ما CHITA را ارائه کردیم، یک رویکرد مبتنی بر بهینه سازی برای هرس شبکه های عصبی از پیش آموزش دیده. CHITA مقیاسپذیری و عملکرد رقابتی را با استفاده کارآمد از اطلاعات مرتبه دوم و استفاده از ایدههای بهینهسازی ترکیبی و آمار با ابعاد بالا ارائه میدهد.
CHITA برای هرس بدون ساختار که در آن می توان هر وزنی را حذف کرد. در تئوری، هرس بدون ساختار می تواند به طور قابل توجهی نیازهای محاسباتی را کاهش دهد. با این حال، تحقق این کاهش ها در عمل نیازمند نرم افزار خاصی (و احتمالاً سخت افزار) است که از محاسبات پراکنده پشتیبانی می کند. متقابلا، هرس ساختاری، که کل ساختارها مانند نورون ها را حذف می کند، ممکن است پیشرفت هایی را ارائه دهد که دستیابی به آنها در نرم افزار و سخت افزار همه منظوره آسان تر است. گسترش CHITA به هرس ساختاری جالب خواهد بود.
سپاسگزاریها
این کار بخشی از یک همکاری تحقیقاتی بین گوگل و MIT است. از راهول مازومدر، ناتالیا پونوماروا، ونیو چن، ژیانگ منگ، ژه ژائو و سرگئی واسیلویتسکی برای کمکشان در تهیه این پست و مقاله تشکر میکنیم. همچنین از John Guilyard برای ایجاد گرافیک در این پست تشکر می کنم.