
مدلهای زبان بزرگ (LLM)، مانند GPT-3 و PaLM، پیشرفت چشمگیری در سالهای اخیر نشان دادهاند که با افزایش مقیاس مدلها و اندازه دادههای آموزشی هدایت شدهاند. با این وجود، یک بحث طولانی مدت این است که آیا LLM ها می توانند به طور نمادین استدلال کنند (یعنی دستکاری نمادها بر اساس قوانین منطقی). به عنوان مثال، LLM ها می توانند عملیات ساده حسابی را زمانی که اعداد کوچک هستند، انجام دهند، اما برای انجام با اعداد بزرگ مشکل دارند. این نشان می دهد که LLMها قوانین اساسی مورد نیاز برای انجام این عملیات حسابی را نیاموخته اند.
در حالی که شبکههای عصبی دارای قابلیتهای تطبیق الگوی قدرتمندی هستند، اما مستعد تطبیق بیش از حد با الگوهای آماری جعلی در دادهها هستند. هنگامی که داده های آموزشی بزرگ و متنوع هستند و ارزیابی در توزیع است، این مانع عملکرد خوب نمی شود. با این حال، برای کارهایی که نیاز به استدلال مبتنی بر قاعده دارند (مانند اضافه کردن)، LLM ها با تعمیم خارج از توزیع دست و پنجه نرم می کنند، زیرا همبستگی های جعلی در داده های آموزشی اغلب بسیار آسان تر از راه حل مبتنی بر قانون واقعی است. در نتیجه، علیرغم پیشرفت قابل توجه در انواع وظایف پردازش زبان طبیعی، عملکرد در کارهای ساده حسابی مانند جمع همچنان یک چالش باقی مانده است. حتی با بهبود اندک GPT-4 در مجموعه داده MATH، خطاها همچنان عمدتاً به دلیل اشتباهات حسابی و محاسباتی است. بنابراین، یک سوال مهم این است که آیا LLM ها قادر به استدلال الگوریتمی هستند، که شامل حل یک کار با اعمال مجموعه ای از قوانین انتزاعی است که الگوریتم را تعریف می کند.
در “آموزش استدلال الگوریتمی از طریق یادگیری درون متنی”، ما رویکردی را توصیف می کنیم که از یادگیری درون زمینه ای برای فعال کردن قابلیت های استدلال الگوریتمی در LLM استفاده می کند. یادگیری درون زمینه ای به توانایی یک مدل برای انجام یک کار پس از دیدن چند نمونه از آن در بافت مدل اشاره دارد. کار با استفاده از یک اعلان برای مدل مشخص می شود، بدون نیاز به به روز رسانی وزن. ما همچنین یک تکنیک تحریک الگوریتمی جدید را ارائه میدهیم که مدلهای زبان هدف کلی را قادر میسازد تا به تعمیم قوی در مسائل حسابی دست یابند که دشوارتر از آنچه در اعلان دیده میشود، دست یابند. در نهایت، ما نشان میدهیم که یک مدل میتواند الگوریتمهایی را بهطور قابل اعتمادی روی نمونههای خارج از توزیع با انتخاب مناسب استراتژی تحریک اجرا کند.
 |
| با ارائه اعلانهای الگوریتمی، میتوانیم قواعد محاسباتی را از طریق یادگیری درون متنی به یک مدل آموزش دهیم. در این مثال، LLM (پیشبینیکننده کلمه) وقتی با یک سؤال جمع آسان (مثلاً 267+197) از شما خواسته میشود، پاسخ صحیح را ارائه میدهد، اما وقتی سؤال جمعآوری مشابه با ارقام طولانیتر پرسیده میشود، با شکست مواجه میشود. با این حال، هنگامی که سؤال دشوارتر با یک دستور الگوریتمی برای جمع اضافه می شود (جعبه آبی با سفید + در زیر کلمه پیش بینی نشان داده شده است)، مدل قادر است به درستی پاسخ دهد. علاوه بر این، مدل قادر به شبیه سازی الگوریتم ضرب (ایکس) با ترکیب یک سری محاسبات جمع. |
آموزش الگوریتم به عنوان یک مهارت
به منظور آموزش الگوریتم به مدل به عنوان یک مهارت، ما اعلان الگوریتمی را توسعه میدهیم که بر اساس سایر رویکردهای تقویتشده منطقی (مثلاً صفحه خراش و زنجیرهای از فکر) استوار است. تحریک الگوریتمی تواناییهای استدلال الگوریتمی را از LLMها استخراج میکند و دو تمایز قابلتوجه در مقایسه با سایر رویکردهای تحریککننده دارد: (1) وظایف را با خروجیدادن مراحل مورد نیاز برای یک راهحل الگوریتمی حل میکند، و (2) هر مرحله الگوریتمی را با جزئیات کافی توضیح میدهد. جایی برای تفسیر نادرست توسط LLM وجود ندارد.
برای به دست آوردن شهود برای تحریک الگوریتمی، بیایید وظیفه جمع دو عدد را در نظر بگیریم. در یک درخواست به سبک اسکرچپد، هر رقم را از راست به چپ پردازش میکنیم و ارزش حمل را دنبال میکنیم (یعنی اگر رقم فعلی بزرگتر از 9 باشد یک عدد 1 به رقم بعدی اضافه میکنیم) در هر مرحله. با این حال، قاعده حمل پس از مشاهده تنها چند نمونه از ارزش حمل مبهم است. ما متوجه شدیم که شامل معادلات صریح برای توصیف قانون حمل به مدل کمک می کند تا بر جزئیات مربوطه تمرکز کند و اعلان را با دقت بیشتری تفسیر کند. ما از این بینش برای ایجاد یک دستور الگوریتمی برای جمع دو عدد استفاده میکنیم، که در آن معادلات صریح را برای هر مرحله از محاسبه ارائه میکنیم و عملیات نمایهسازی مختلف را در قالبهای غیر مبهم توصیف میکنیم.
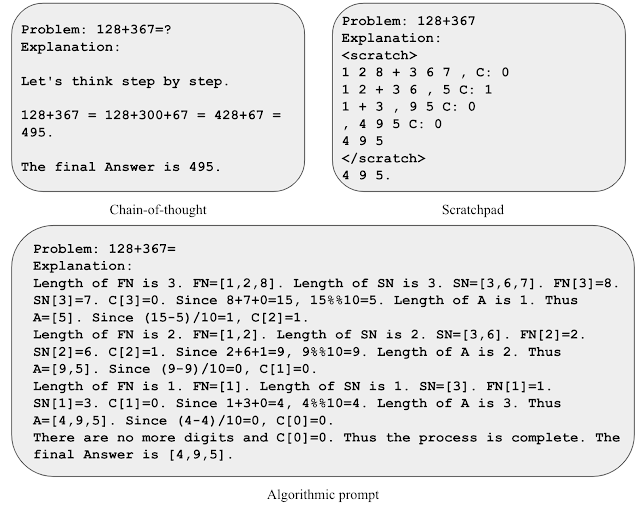 |
| تصویری از استراتژی های مختلف سریع برای اضافه کردن. |
تنها با استفاده از سه مثال سریع از جمع با طول پاسخ تا پنج رقم، عملکرد را در جمعهای تا 19 رقم ارزیابی میکنیم. دقت بیش از 2000 نمونه نمونه به طور یکنواخت در طول پاسخ اندازه گیری می شود. همانطور که در زیر نشان داده شده است، استفاده از اعلان های الگوریتمی دقت بالایی را برای سوالات به میزان قابل توجهی طولانی تر از آنچه در اعلان مشاهده می شود حفظ می کند، که نشان می دهد مدل در واقع با اجرای یک الگوریتم ورودی-آگنوستیک، کار را حل می کند.
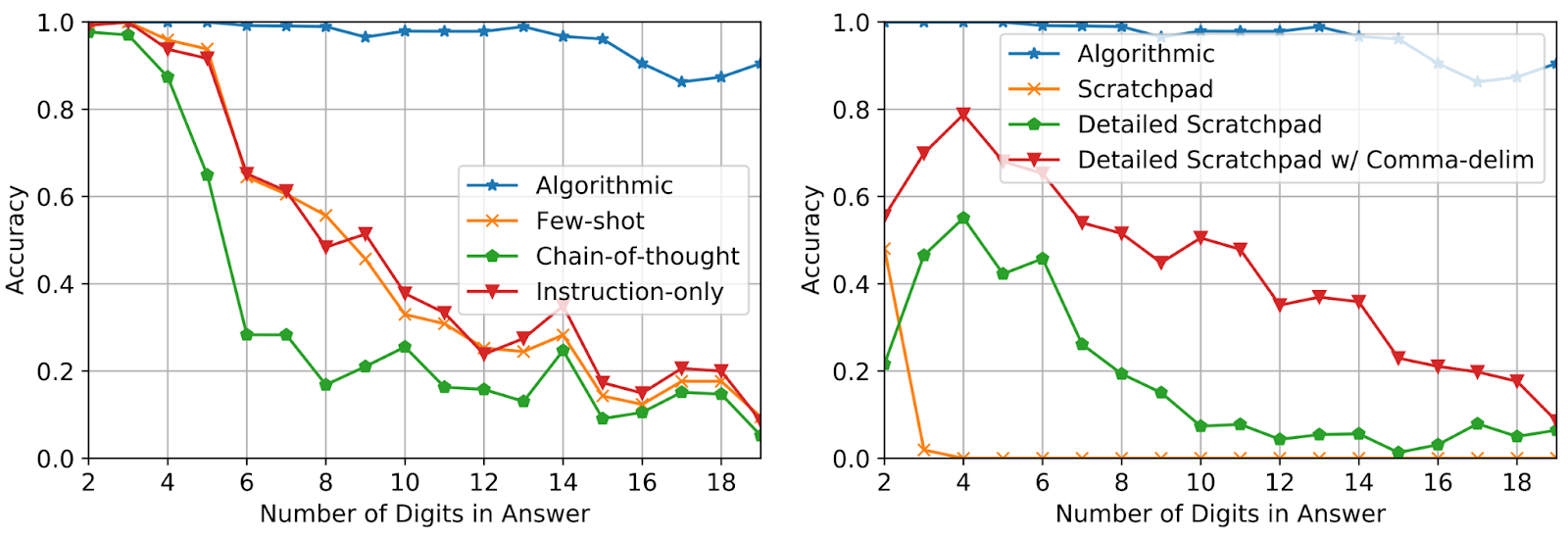 |
| آزمون دقت در سوالات جمع افزایش طول برای روش های مختلف تحریک. |
استفاده از مهارت های الگوریتمی به عنوان استفاده از ابزار
برای ارزیابی اینکه آیا این مدل میتواند از استدلال الگوریتمی در یک فرآیند استدلال گستردهتر استفاده کند، عملکرد را با استفاده از مسائل کلمه ریاضی مدرسه (GSM8k) ارزیابی میکنیم. ما به طور خاص سعی می کنیم محاسبات جمع را از GSM8k با یک راه حل الگوریتمی جایگزین کنیم.
با انگیزه محدودیتهای طول زمینه و تداخل احتمالی بین الگوریتمهای مختلف، ما استراتژی را بررسی میکنیم که در آن مدلهای متفاوت با یکدیگر برای حل وظایف پیچیده تعامل دارند. در زمینه GSM8k، ما یک مدل داریم که در استدلال ریاضی غیررسمی با استفاده از تحریک زنجیرهای از فکر تخصص دارد، و مدل دومی که علاوه بر استفاده از تحریک الگوریتمی، متخصص است. از مدل استدلال ریاضی غیررسمی خواسته میشود تا توکنهای تخصصی را به منظور فراخوانی مدل جمعآوریشده برای انجام مراحل حسابی، خروجی دهد. کوئریها را بین توکنها استخراج میکنیم، آنها را به مدل اضافه میفرستیم و پاسخ را به مدل اول برمیگردانیم و پس از آن مدل اول خروجی خود را ادامه میدهد. ما رویکرد خود را با استفاده از یک مسئله دشوار از GSM8k (GSM8k-Hard) ارزیابی می کنیم، جایی که به طور تصادفی 50 سؤال فقط جمع را انتخاب می کنیم و مقادیر عددی سؤالات را افزایش می دهیم.
 |
| نمونه ای از مجموعه داده GSM8k-Hard. اعلان زنجیرهای از فکر با براکتهایی افزوده میشود تا نشان دهد چه زمانی باید یک فراخوانی الگوریتمی انجام شود. |
ما متوجه شدیم که استفاده از زمینهها و مدلهای جداگانه با اعلانهای تخصصی یک راه مؤثر برای مقابله با GSM8k-Hard است. در زیر مشاهده می کنیم که عملکرد مدل با فراخوان الگوریتمی برای جمع 2.3 برابر خط پایه زنجیره فکر است. در نهایت، این استراتژی نمونه ای از حل وظایف پیچیده را با تسهیل تعاملات بین LLM های تخصصی به مهارت های مختلف از طریق یادگیری درون زمینه ای ارائه می دهد.
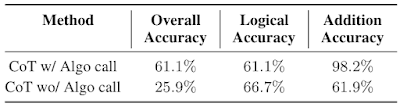 |
| عملکرد Chain-of-thought (CoT) در GSM8k-Hard با یا بدون تماس الگوریتمی. |
نتیجه
ما رویکردی را ارائه میدهیم که از یادگیری درون متنی و یک تکنیک تحریک الگوریتمی جدید برای باز کردن تواناییهای استدلال الگوریتمی در LLM استفاده میکند. نتایج ما نشان می دهد که ممکن است با ارائه توضیحات دقیق تر، زمینه طولانی تر را به عملکرد استدلال بهتر تبدیل کنیم. بنابراین، این یافتهها به توانایی استفاده یا شبیهسازی زمینههای طولانی و ایجاد دلایل آموزندهتر به عنوان جهتهای پژوهشی امیدوارکننده اشاره میکنند.
سپاسگزاریها
ما از نویسندگان همکارمان بهنام نیشابور، آزاده نوا، هوگو لاروشل و آرون کورویل به خاطر مشارکت ارزشمندشان در مقاله و بازخورد عالی در وبلاگ تشکر می کنیم. از تام اسمال برای ساخت انیمیشن های این پست تشکر می کنیم. این کار در دوره کارآموزی Hattie Zhou در Google Research انجام شد.