به عنوان بخشی از مجموعه آموزشهای PCA با پایتون، تکنیکهای مختلف تجسم دادهها را یاد میگیریم که میتوان با تجزیه و تحلیل اجزای اصلی از آنها استفاده کرد.
در این بخش، تکنیکها و نمودارهای مختلف تجسم دادهها را یاد میگیریم که میتوانید برای به دست آوردن بینش از دادههای PCA خود استفاده کنید، مانند:
- نمودار نوار واریانس توضیح داده شده با ویژگی
- طرح PCA Scree
- طرح پراکندگی PCA سه بعدی
- طرح پراکندگی 2 بعدی PCA
- دوبعدی PCA Biplot
- PCA 3D Biplot
ما کاهش ابعاد را با PCA در مجموعه داده Iris انجام خواهیم داد.
تجسم تجزیه و تحلیل اجزای اصلی با پایتون
تجسم داده ها با استفاده از PCA در پایتون به درک داده های پیچیده کمک می کند. با استفاده از تجزیه و تحلیل اجزای اصلی در Scikit-learn، میتوانیم تمام اطلاعاتی را که در اختیار داریم استفاده کرده و آنها را در مهمترین اجزای آن سادهسازی کنیم.
بارگیری مجموعه داده Iris در پایتون
برای شروع، مجموعه داده Iris را در پایتون بارگذاری می کنیم، مقداری پیش پردازش انجام می دهیم و از PCA برای کاهش مجموعه داده به 3 ویژگی استفاده می کنیم. برای اینکه بدانید این به چه معناست، آموزش ما در مورد PCA با پایتون را دنبال کنید.
import pandas as pd
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# load features and targets separately
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Data Scaling
x_scaled = StandardScaler().fit_transform(X)
# Reduce from 4 to 3 features with PCA
pca = PCA(n_components=3)
# Fit and transform data
pca_features = pca.fit_transform(x_scaled)
از این داده ها، ما روش های مختلفی را برای رسم PCA با پایتون یاد خواهیم گرفت.
نحوه رسم واریانس توضیح داده شده در پایتون
واریانس توضیح داده شده در PCA به ما کمک می کند تا بفهمیم چه مقدار اطلاعات پس از کاهش ابعاد حفظ می شود. این بخشی از تغییرپذیری داده های اصلی است که توسط هر جزء اصلی گرفته می شود.
ما می توانیم واریانس توضیح داده شده را رسم کنیم تا واریانس هر ویژگی جزء اصلی را ببینیم.
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# Bar plot of explained_variance
plt.bar(
range(1,len(pca.explained_variance_)+1),
pca.explained_variance_
)
plt.xlabel('PCA Feature')
plt.ylabel('Explained variance')
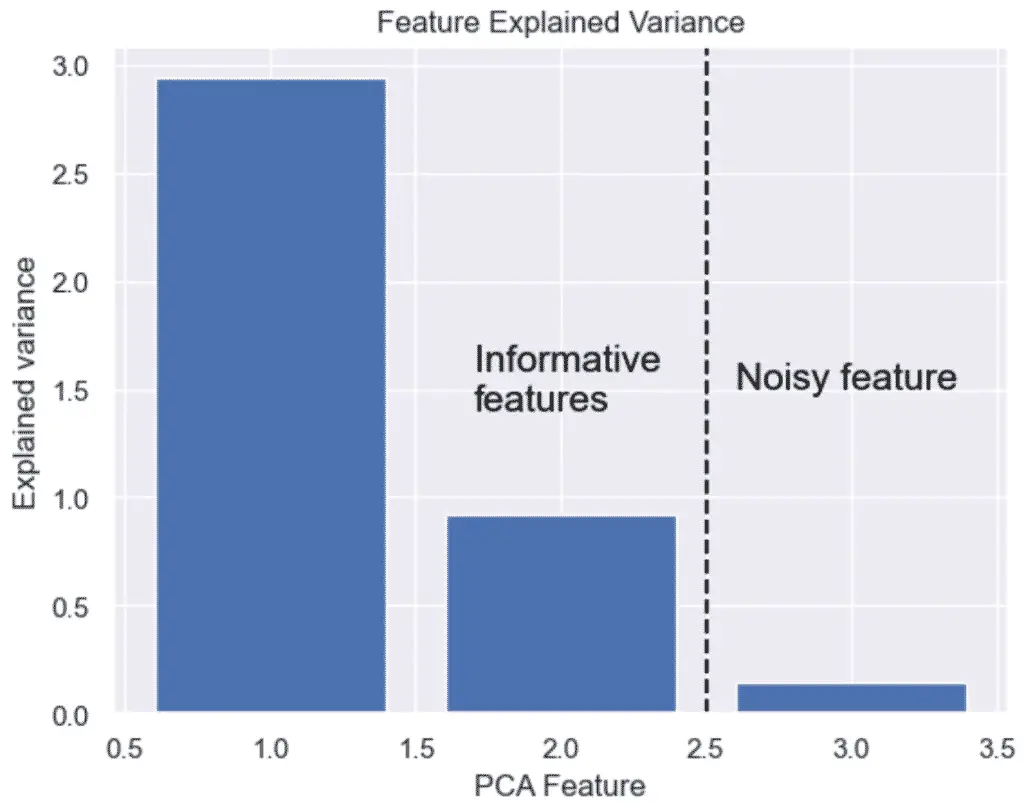
plt.title('Feature Explained Variance')
plt.show()
نمودار خروجی نشان می دهد که ما به 3 ویژگی نیاز نداریم، بلکه فقط به 2 ویژگی نیاز داریم. واریانس ویژگی 3 واضح است که چندان قابل توجه نیست.
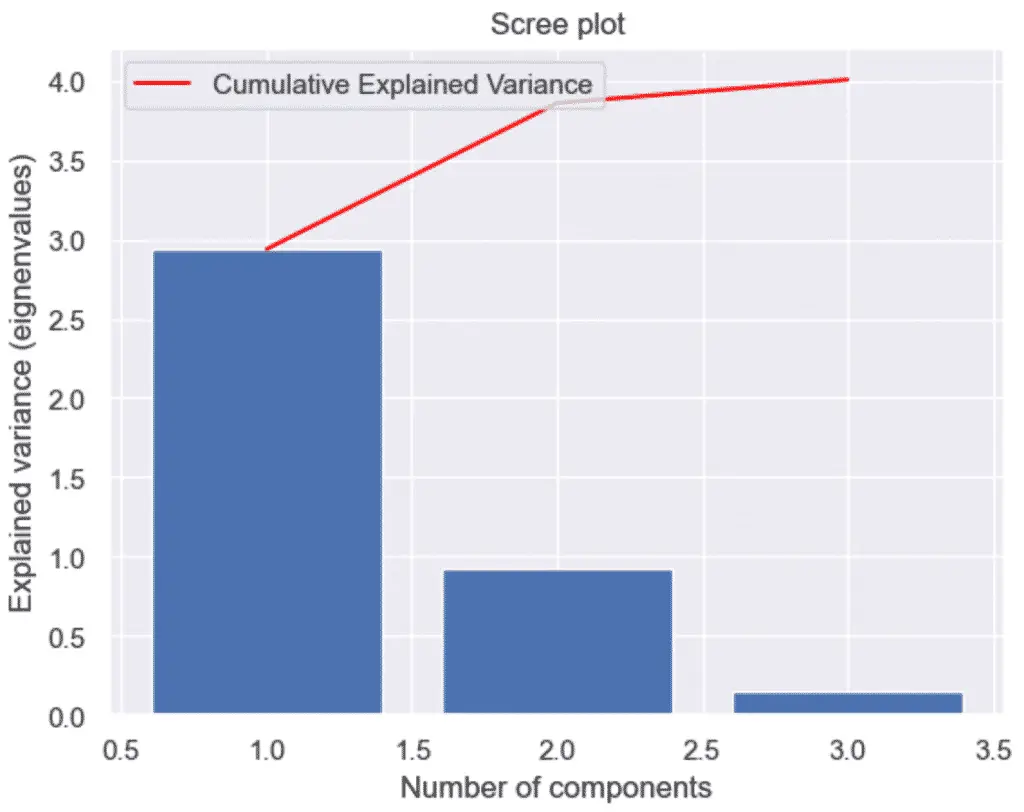
چگونه با پایتون و PCA یک Scree Plot بسازیم
برای ایجاد یک نمودار اسکری یا نمودار واریانس توضیح تجمعی، با پایتون و PCA، ابتدا یک نمودار نوار واریانس توضیح داده شده را رسم کنید و یک نمودار ثانویه از مجموع تجمعی اضافه کنید، که به عنوان واریانس توضیح داده شده تجمعی نیز شناخته می شود.
نمودار اسکری چیزی نیست جز نمودار مقادیر ویژه (که به عنوان واریانس توضیح داده شده نیز شناخته می شود). اساساً، همان اطلاعات طرح بالا را ارائه می دهد.
چرا یک طرح نمایشی بسازیم؟
تجسمهای دوبعدی تجزیه و تحلیل مؤلفههای اصلی تنها در صورتی مرتبط هستند که هر مؤلفه اصلی به اندازه کافی از واریانس دادههای اصلی را دریافت کند. اگر نه، تجسم گمراه کننده خواهد بود.
اضافه کردن مجموع تجمعی واریانس توضیح داده شده می تواند به انجام تست های آرنج برای شناسایی مولفه های اصلی واریانس کم کمک کند.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# Scree Plot
import numpy as np
# Bar plot of explained_variance
plt.bar(
range(1,len(pca.explained_variance_)+1),
pca.explained_variance_
)
plt.plot(
range(1,len(pca.explained_variance_ )+1),
np.cumsum(pca.explained_variance_),
c='red',
label='Cumulative Explained Variance')
plt.legend(loc='upper left')
plt.xlabel('Number of components')
plt.ylabel('Explained variance (eignenvalues)')
plt.title('Scree plot')
plt.show()
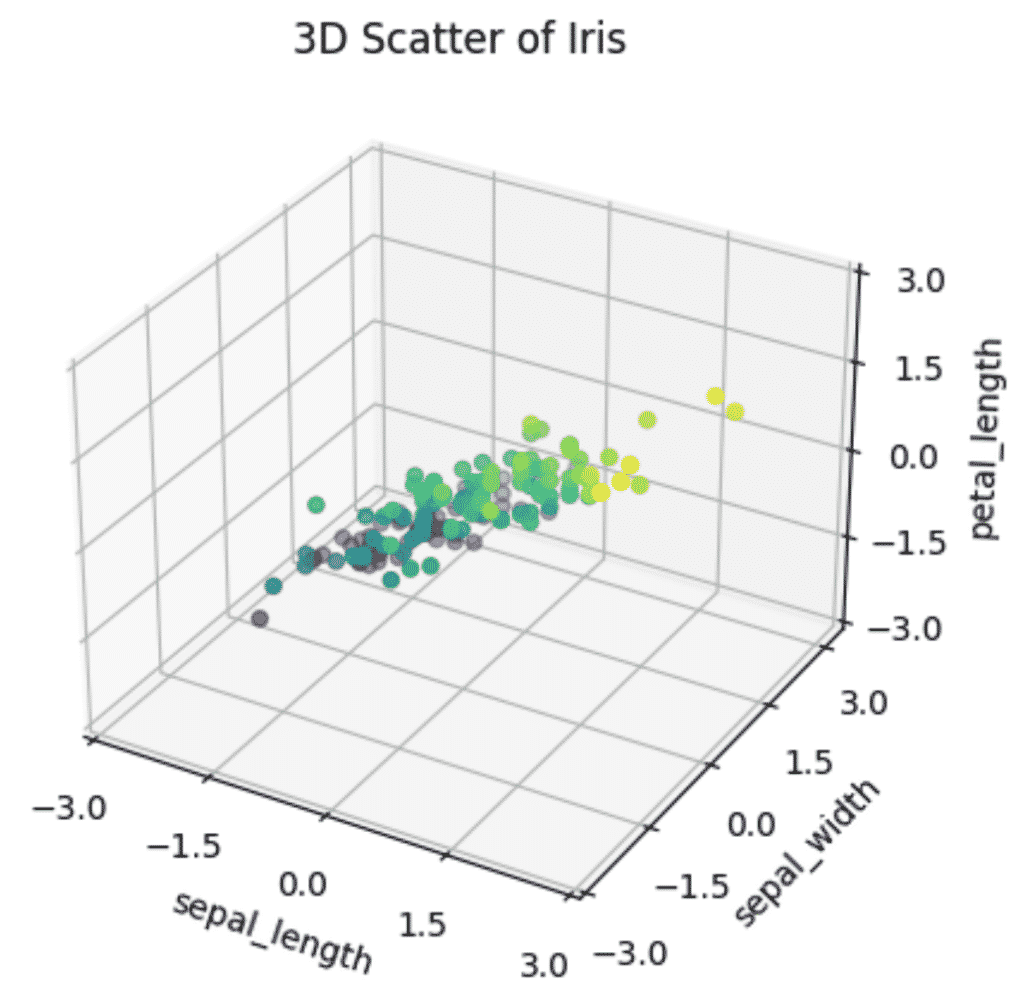
نحوه رسم نمودار سه بعدی PCA در پایتون
برای ترسیم نمودار سه بعدی PCA Scatter در پایتون، یک محیط ترسیم سه بعدی را در آن راه اندازی کنید matplotlib استفاده كردن plt.axes(projection='3d') و ویژگی های PCA خود را در اختیار شما قرار دهید scatter3D روش شی تبر.
ax = plt.axes(projection='3d')
ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='viridis')بیایید با ترسیم ویژگی های انتخاب شده در یک نمودار سه بعدی، یک مثال را ببینیم.
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('default')
# Prepare 3D graph
fig = plt.figure()
ax = plt.axes(projection='3d')
# Plot scaled features
xdata = pca_features[:,0]
ydata = pca_features[:,1]
zdata = pca_features[:,2]
# Plot 3D plot
ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='viridis')
# Plot title of graph
plt.title(f'3D Scatter of Iris')
# Plot x, y, z even ticks
ticks = np.linspace(-3, 3, num=5)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
ax.set_zticks(ticks)
# Plot x, y, z labels
ax.set_xlabel('sepal_length', rotation=150)
ax.set_ylabel('sepal_width')
ax.set_zlabel('petal_length', rotation=60)
plt.show()
هنگام ترسیم یک نمودار سه بعدی، واضح تر است که واریانس کمتری در آن وجود دارد Petal length از گل زنبق نسبت به در Sepal length یا Sepal width، تقریباً یک صفحه دو بعدی مسطح در داخل نمودار سه بعدی ایجاد می کند. این نشان می دهد که بعد ذاتی داده ها به جای 4، اساساً 2 بعد است.
کاهش این 3 ویژگی به 2 نه تنها مدل را سریعتر میکند، بلکه تجسمها را بدون از دست دادن اطلاعات بسیار آموزندهتر میکند.
نحوه رسم نمودار PCA دو بعدی در پایتون
برای ایجاد یک گراف PCA 2 بعدی در پایتون، 2 جزء اصلی خود را به Seaborn ارسال کنید. lmplot تابع. مطمئن شوید که PCA با استفاده از آن نمونه سازی شده است n_components=2.
sns.lmplot(x='PC1', y='PC2', data=pca_df, ...)نمونه ای از نمودار دو بعدی در PCA با استفاده از Python و Scikit-learn:
import pandas as pd
from sklearn.decomposition import PCA
# Reduce from 4 to 2 features with PCA
pca = PCA(n_components=2)
# Fit and transform data
pca_features = pca.fit_transform(x_scaled)
# Create dataframe
pca_df = pd.DataFrame(
data=pca_features,
columns=['PC1', 'PC2'])
# map target names to PCA features
target_names = {
0:'setosa',
1:'versicolor',
2:'virginica'
}
pca_df['target'] = y
pca_df['target'] = pca_df['target'].map(target_names)
pca_df.head()
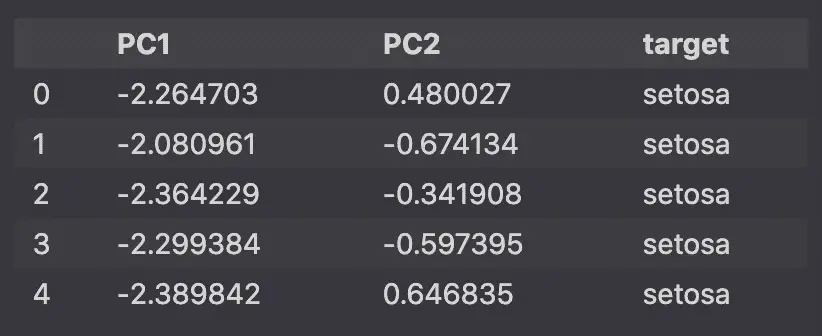
سپس با استفاده از Seaborn’s lmplot، مولفه های اصلی 2 بعدی را روی نمودار پراکندگی رسم می کنیم.
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
sns.lmplot(
x='PC1',
y='PC2',
data=pca_df,
hue='target',
fit_reg=False,
legend=True
)
plt.title('2D PCA Graph')
plt.show()
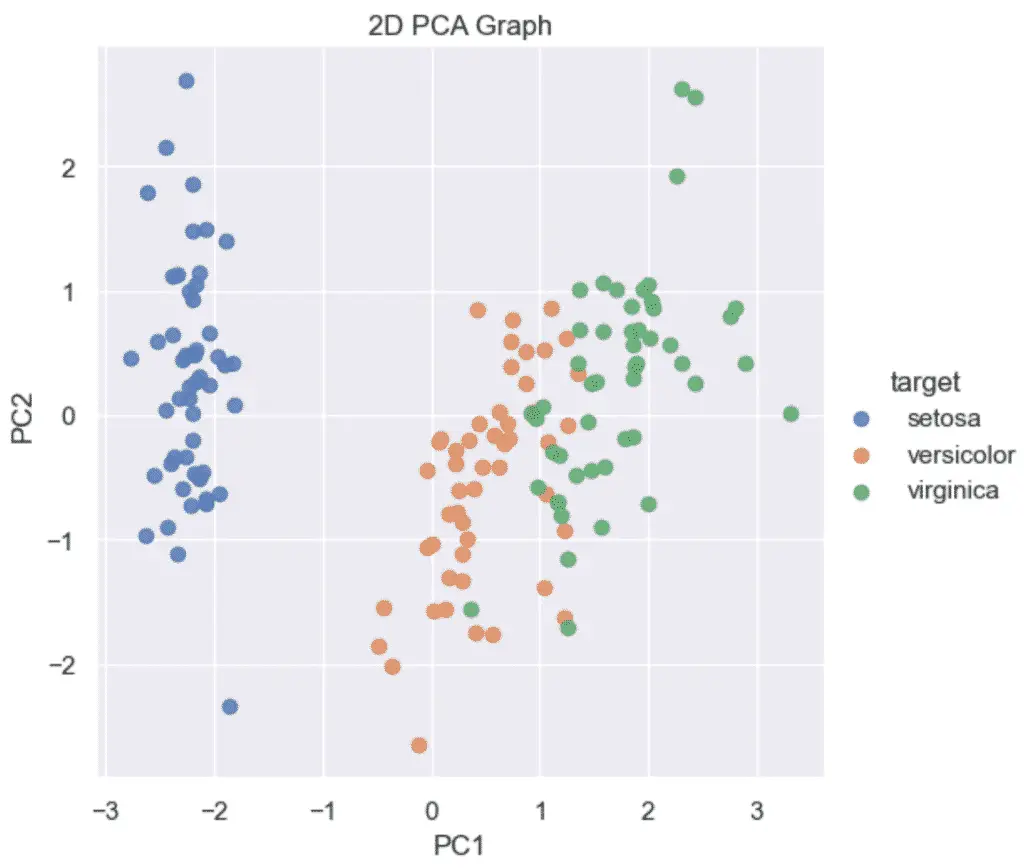
چگونه یک PCA 2D Biplot در پایتون بسازیم؟
یک بای پلات PCA در پایتون، نمودار پراکندگی امتیازات PCA و نمودارهای بارگذاری را ترکیب می کند تا نشان دهد که نقاط داده چگونه با یکدیگر ارتباط دارند.
Biplot نموداری است که نشان می دهد:
- نمودارهای پراکنده PCA مقیاس شده
- کرت های بارگیری علاوه بر این
- بردارهایی که نشان میدهند هر ویژگی چقدر بر مؤلفه اصلی تأثیر میگذارد.
برای تجسم یک Biplot دو بعدی، ابتدا باید یک نمودار بارگذاری و یک نمودار پراکنده از داده های PCA ایجاد کنید و سپس آنها را با یکدیگر ترکیب کنید.
در زیر نمونه ای از نحوه ساخت یک PCA Biplot در پایتون آورده شده است. برای آشنایی بیشتر با نحوه عملکرد کد پایتون مقاله مرتبط را بخوانید.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import pandas as pd
sns.set()
# load features and targets separately
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Scale Data
x_scaled = StandardScaler().fit_transform(X)
# Perform PCA on Scaled Data
pca = PCA(n_components=2)
pca_features = pca.fit_transform(x_scaled)
# Principal components correlation coefficients
loadings = pca.components_
# Number of features before PCA
n_features = pca.n_features_in_
# Feature names before PCA
feature_names = iris.feature_names
# PC names
pc_list = [f'PC{i}' for i in list(range(1, n_features + 1))]
# Match PC names to loadings
pc_loadings = dict(zip(pc_list, loadings))
# Matrix of corr coefs between feature names and PCs
loadings_df = pd.DataFrame.from_dict(pc_loadings)
loadings_df['feature_names'] = feature_names
loadings_df = loadings_df.set_index('feature_names')
# Get the loadings of x and y axes
xs = loadings[0]
ys = loadings[1]
# Create DataFrame from PCA
pca_df = pd.DataFrame(
data=pca_features,
columns=['PC1', 'PC2'])
# Map Targets to names
target_names = {
0:'setosa',
1:'versicolor',
2:'virginica'
}
pca_df['target'] = y
pca_df['target'] = pca_df['target'].map(target_names)
# Scale PCS into a DataFrame
pca_df_scaled = pca_df.copy()
scaler_df = pca_df[['PC1', 'PC2']]
scaler = 1 / (scaler_df.max() - scaler_df.min())
for index in scaler.index:
pca_df_scaled[index] *= scaler[index]
# Plot the loadings on a Scatter plot
xs = loadings[0]
ys = loadings[1]
sns.lmplot(
x='PC1',
y='PC2',
data=pca_df_scaled,
fit_reg=False,
)
for i, varnames in enumerate(feature_names):
plt.scatter(xs[i], ys[i], s=200)
plt.arrow(
0, 0, # coordinates of arrow base
xs[i], # length of the arrow along x
ys[i], # length of the arrow along y
color='r',
head_width=0.01
)
plt.text(xs[i], ys[i], varnames)
xticks = np.linspace(-0.8, 0.8, num=5)
yticks = np.linspace(-0.8, 0.8, num=5)
plt.xticks(xticks)
plt.yticks(yticks)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.title('2D Biplot')
plt.show()
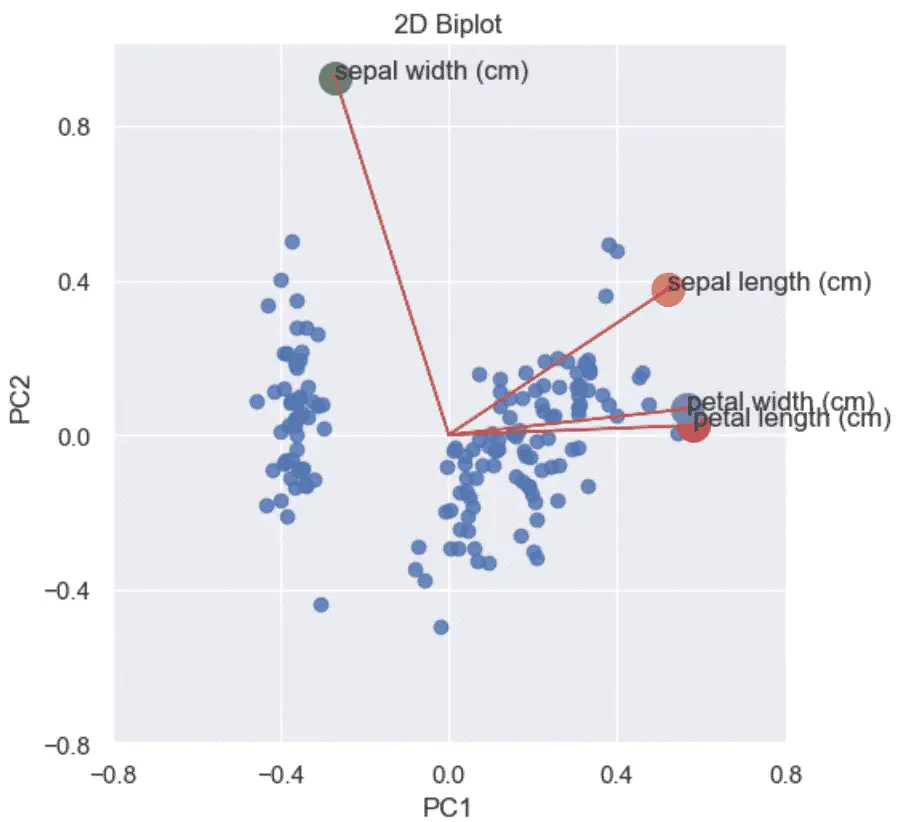
چگونه یک PCA 3D Biplot در پایتون بسازیم؟
بای پلات سه بعدی تمام مراحل بالا را با استفاده از 3 جزء به جای 2 ترکیب می کند.
import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
plt.style.use('default')
# load features and targets separately
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Scale Data
x_scaled = StandardScaler().fit_transform(X)
pca = PCA(n_components=3)
# Fit and transform data
pca_features = pca.fit_transform(x_scaled)
# Create dataframe
pca_df = pd.DataFrame(
data=pca_features,
columns=['PC1', 'PC2', 'PC3'])
# map target names to PCA features
target_names = {
0:'setosa',
1:'versicolor',
2:'virginica'
}
# Apply the targett names
pca_df['target'] = iris.target
pca_df['target'] = pca_df['target'].map(target_names)
# Create the scaled PCA dataframe
pca_df_scaled = pca_df.copy()
scaler_df = pca_df[['PC1', 'PC2', 'PC3']]
scaler = 1 / (scaler_df.max() - scaler_df.min())
for index in scaler.index:
pca_df_scaled[index] *= scaler[index]
# Initialize the 3D graph
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Define scaled features as arrays
xdata = pca_df_scaled['PC1']
ydata = pca_df_scaled['PC2']
zdata = pca_df_scaled['PC3']
# Plot 3D scatterplot of PCA
ax.scatter3D(
xdata,
ydata,
zdata,
c=zdata,
cmap='Greens',
alpha=0.5)
# Define the x, y, z variables
loadings = pca.components_
xs = loadings[0]
ys = loadings[1]
zs = loadings[2]
# Plot the loadings
for i, varnames in enumerate(feature_names):
ax.scatter(xs[i], ys[i], zs[i], s=200)
ax.text(
xs[i] + 0.1,
ys[i] + 0.1,
zs[i] + 0.1,
varnames)
# Plot the arrows
x_arr = np.zeros(len(loadings[0]))
y_arr = z_arr = x_arr
ax.quiver(x_arr, y_arr, z_arr, xs, ys, zs)
# Plot title of graph
plt.title(f'3D Biplot of Iris')
# Plot x, y, z labels
ax.set_xlabel('Principal component 1', rotation=150)
ax.set_ylabel('Principal component 2')
ax.set_zlabel('Principal component 3', rotation=60)
plt.show()
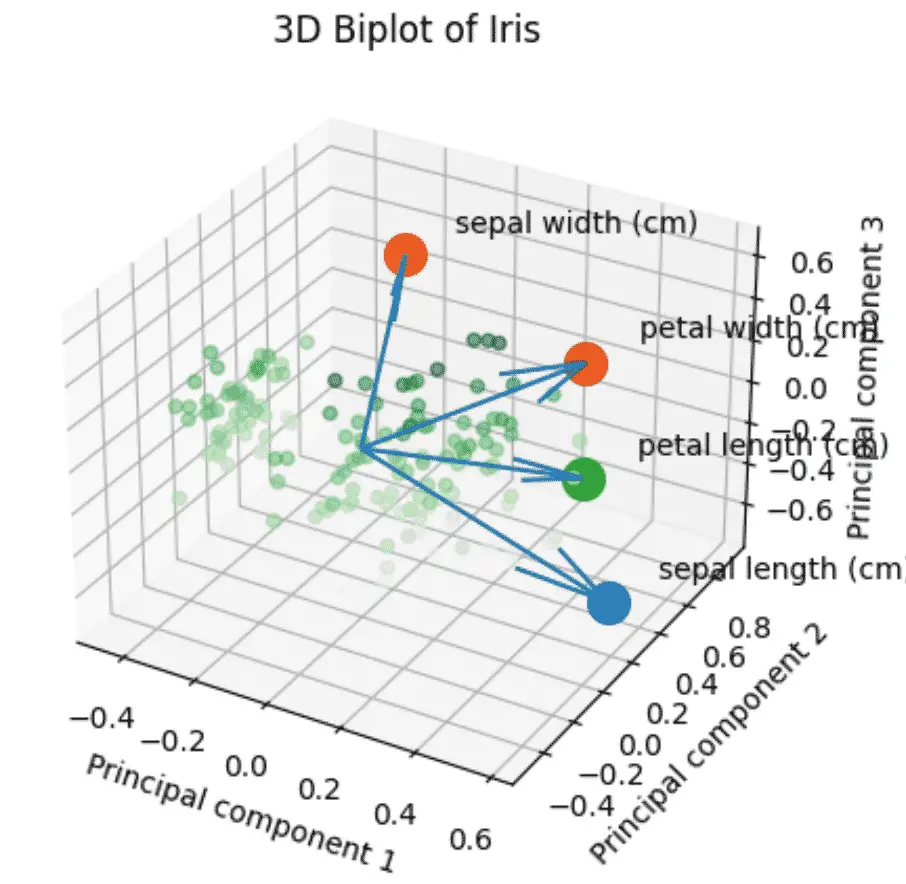

استراتژیست سئو در Tripadvisor، Seek سابق (ملبورن، استرالیا). متخصص در سئو فنی. نویسنده در پایتون، بازیابی اطلاعات، سئو و یادگیری ماشین. نویسنده مهمان در SearchEngineJournal، SearchEngineLand و OnCrawl.