میانه خصوصی متفاوت و بیشتر – وبلاگ تحقیقاتی گوگل

ارسال شده توسط ادیت کوهن و اوری استمر، دانشمندان تحقیقاتی، تحقیقات گوگل

حریم خصوصی دیفرانسیل (DP) یک تعریف ریاضی دقیق از حریم خصوصی است. الگوریتم‌های DP برای محافظت از داده‌های کاربر با اطمینان از اینکه احتمال خروجی خاصی تقریباً بدون تغییر در هنگام اضافه یا حذف یک نقطه داده، محافظت می‌شوند، تصادفی می‌شوند. بنابراین، خروجی یک الگوریتم DP وجود یک نقطه داده را آشکار نمی کند. پیشرفت قابل توجهی هم در تحقیقات بنیادی و هم در پذیرش حریم خصوصی متمایز با مشارکت هایی مانند Privacy Sandbox و Google Source Open Library حاصل شده است.

الگوریتم‌های ML و تجزیه و تحلیل داده‌ها را اغلب می‌توان به عنوان انجام چندین مرحله محاسباتی اساسی بر روی یک مجموعه داده توصیف کرد. هنگامی که هر مرحله به طور متفاوت خصوصی است، خروجی نیز خصوصی است، اما با چند مرحله، حریم خصوصی را تضمین می کند خراب می شود، پدیده ای که به نام هزینه ترکیب. قضایای ترکیب، افزایش از دست دادن حریم خصوصی را با عدد مرتبط می کند ک از محاسبات: در حالت کلی، از دست دادن حریم خصوصی با ریشه دوم افزایش می یابد ک. این به این معنی است که ما برای هر مرحله به ضمانت‌های حفظ حریم خصوصی بسیار سخت‌گیرانه‌تری نیاز داریم تا به هدف کلی تضمین حریم خصوصی خود برسیم. اما در این صورت، ما سودمندی را از دست می دهیم. یکی از راه‌های بهبود مبادله حریم خصوصی در مقابل سودمندی، شناسایی زمانی است که موارد استفاده، تحلیل حریم خصوصی دقیق‌تری را نسبت به آنچه از قضایای ترکیب به دست می‌آید تایید می‌کنند.

کاندیدهای خوب برای چنین بهبودی زمانی هستند که هر مرحله بر روی یک بخش (برش) جدا از مجموعه داده اعمال شود. هنگامی که برش ها به روشی مستقل از داده انتخاب می شوند، هر نقطه تنها بر یکی از آنها تأثیر می گذارد ک خروجی ها و تضمین های حفظ حریم خصوصی بدتر نمی شوند ک. با این حال، برنامه هایی وجود دارند که در آنها باید برش ها را به صورت تطبیقی ​​انتخاب کنیم (یعنی به روشی که به خروجی مراحل قبلی بستگی دارد). در این موارد، تغییر یک نقطه داده منفرد ممکن است آبشاری کند – تغییر چند برش و در نتیجه افزایش هزینه ترکیب.

در «یادگیری خصوصی متفاوت آستانه‌ها و بهینه‌سازی شبه مقعر» که در STOC 2023 ارائه شد، الگوی جدیدی را توصیف می‌کنیم که به برش‌ها اجازه می‌دهد به صورت تطبیقی ​​انتخاب شوند و در عین حال از هزینه ترکیب جلوگیری می‌کنند. ما نشان می‌دهیم که الگوریتم‌های DP برای تجمیع اساسی و وظایف یادگیری را می‌توان در این پارادایم Reorder-Slice-Compute (RSC) بیان کرد و پیشرفت‌های قابل‌توجهی در ابزار به دست آورد.

پارادایم Reorder-Slice-Compute (RSC).

یک الگوریتم آ اگر بتوان آن را به شکل کلی زیر بیان کرد، در پارادایم RSC قرار می گیرد (به تجسم زیر مراجعه کنید). ورودی یک مجموعه حساس است D از نقاط داده سپس الگوریتم دنباله ای از ک مراحل به شرح زیر است:

1. یک سفارش را از روی نقاط داده، یک اندازه برش انتخاب کنید مترو یک الگوریتم DP م. انتخاب ممکن است به خروجی بستگی داشته باشد آ در مراحل قبلی (و از این رو تطبیقی ​​است).
2. قسمت بالایی (تقریباً) را برش دهید متر نقاط داده با توجه به ترتیب از مجموعه داده D، درخواست دادن م به برش، و خروجی نتیجه.

تجسم سه مرحله Reorder-Slice-Compute (RSC).

اگر از دست دادن حریم خصوصی یک الگوریتم RSC را با استفاده از قضایای ترکیب DP تجزیه و تحلیل کنیم، تضمین حریم خصوصی از هزینه ترکیب مورد انتظار رنج می برد، یعنی با جذر تعداد مراحل بدتر می شود. ک. برای حذف این هزینه ترکیب، ما یک تحلیل جدید ارائه می کنیم که وابستگی به آن را حذف می کند ک در مجموع: تضمین حریم خصوصی به طور کلی نزدیک به یک مرحله است! ایده پشت تجزیه و تحلیل دقیق تر ما یک تکنیک جدید است که آبشار بالقوه گام های تحت تأثیر را هنگامی که یک نقطه داده منفرد اصلاح می شود (جزئیات در مقاله) محدود می کند.

تجزیه و تحلیل حریم خصوصی دقیق تر به معنای استفاده بهتر است. اثربخشی الگوریتم‌های DP اغلب بر حسب کوچک‌ترین اندازه ورودی (تعداد نقاط داده) بیان می‌شود که برای انتشار یک نتیجه صحیح که شرایط حریم خصوصی را برآورده می‌کند، کافی است. ما چندین مشکل را با الگوریتم‌هایی توصیف می‌کنیم که می‌توانند در پارادایم RSC بیان شوند و تجزیه و تحلیل دقیق‌تر ما برای آنها سودمندی را بهبود بخشید.

نقطه فاصله خصوصی

ما با کار تجمیع اولیه زیر شروع می کنیم. ورودی یک مجموعه داده است D از n امتیاز از دامنه سفارش داده شده ایکس (دامنه را به عنوان اعداد طبیعی بین در نظر بگیرید 1 و |X|). هدف برگرداندن یک امتیاز است y که در ایکس که در فاصله از D، که بین حداقل و حداکثر امتیاز در است D.

راه حل مشکل نقطه فاصله بدون نیاز به حریم خصوصی بی اهمیت است: به سادگی هر نقطه از مجموعه داده را برگردانید D. اما این راه حل حفظ حریم خصوصی نیست زیرا وجود یک نقطه داده خاص را در ورودی فاش می کند. همچنین می‌توانیم ببینیم که اگر تنها یک نقطه در مجموعه داده وجود داشته باشد، راه‌حل حفظ حریم خصوصی ممکن نیست، زیرا باید آن نقطه را برگرداند. بنابراین می‌توانیم سؤال اساسی زیر را بپرسیم: کوچکترین اندازه ورودی چیست؟ ن که برای آن می توانیم مشکل نقطه فاصله خصوصی را حل کنیم؟

مشخص است که ن باید با اندازه دامنه افزایش یابد |X| و اینکه این وابستگی حداقل تابع log تکرار شده است ورود به سیستم* |X| [1, 2]. از سوی دیگر، بهترین الگوریتم DP قبلی نیاز داشت که اندازه ورودی حداقل (log* |X|)^1.5. برای از بین بردن این شکاف، یک الگوریتم RSC طراحی کردیم که فقط به ترتیب ثبت نیاز دارد* |X| نکته ها.

تابع log تکرار شده بسیار کند در حال رشد است: تعداد دفعاتی است که باید لگاریتم یک مقدار را قبل از رسیدن به مقداری مساوی یا کوچکتر از آن بگیریم. 1. چگونه این تابع به طور طبیعی در تجزیه و تحلیل ظاهر شد؟ هر مرحله از الگوریتم RSC، دامنه را به لگاریتمی با اندازه قبلی خود بازنگری می کند. بنابراین ورود به سیستم وجود دارد * |X| در مجموع مراحل تجزیه و تحلیل دقیق تر RSC یک جذر از تعداد مراحل را از اندازه ورودی مورد نیاز حذف کرد.

حتی اگر وظیفه نقطه فاصله بسیار اساسی به نظر می رسد، ماهیت دشواری راه حل های خصوصی برای وظایف تجمیع مشترک را نشان می دهد. در ادامه دو مورد از این وظایف را شرح می دهیم و اندازه ورودی مورد نیاز برای این وظایف را بر حسب بیان می کنیم ن.

میانگین تقریبی خصوصی

یکی از این کارهای رایج تجمیع این است میانه تقریبی: ورودی یک مجموعه داده است D از n امتیاز از دامنه سفارش داده شده ایکس. هدف برگرداندن یک امتیاز است y که بین چندک های ⅓ و ⅔ است D. یعنی حداقل یک سوم از نقاط در D کوچکتر یا مساوی هستند y و حداقل یک سوم نقاط بزرگتر یا مساوی باشند y. توجه داشته باشید که بازگرداندن یک میانه دقیق با حریم خصوصی دیفرانسیل امکان پذیر نیست، زیرا وجود یک نقطه داده را فاش می کند. از این رو ما نیاز آرام یک میانه تقریبی را در نظر می گیریم (در زیر نشان داده شده است).

ما می‌توانیم یک میانه تقریبی را با پیدا کردن یک نقطه فاصله محاسبه کنیم: ما آن را برش می‌زنیم ن کوچکترین نقاط و ن بزرگترین نقاط و سپس یک نقطه فاصله از نقاط باقی مانده را محاسبه کنید. مورد دوم باید یک میانه تقریبی باشد. این زمانی کار می کند که اندازه مجموعه داده حداقل باشد 3N.

مثالی از یک داده D روی دامنه X، مجموعه نقاط بازه و مجموعه میانه های تقریبی.

یادگیری خصوصی مستطیل های تراز محور

برای کار بعدی، ورودی مجموعه ای از n نقاط داده برچسب گذاری شده، جایی که هر نقطه x = (x₁،….،ایکس_د) هست یک د-بردار بعدی روی یک دامنه ایکس. در زیر نشان داده شده است، هدف یادگیری ارزش ها است آ_من ، ب_من برای محورها i=1,…,d که الف را تعریف می کنند د-بعدی مستطیل، به طوری که برای هر مثال ایکس

• اگر ایکس به صورت مثبت برچسب گذاری شده است (به عنوان علائم قرمز به علاوه در زیر نشان داده شده است) سپس در داخل مستطیل قرار می گیرد، یعنی برای همه محورها من، ایکس_من در فاصله است [a_i ,b_i]، و
• اگر ایکس دارای برچسب منفی است (در زیر به صورت علائم منهای آبی نشان داده شده است) سپس خارج از مستطیل قرار دارد، یعنی حداقل برای یک محور من، ایکس_من خارج از فاصله است [a_i ,b_i].

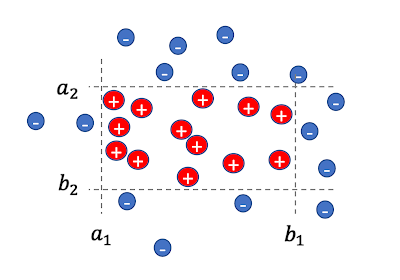مجموعه ای از نقاط برچسب گذاری شده دو بعدی و یک مستطیل مربوطه.

هر راه حل DP برای این مشکل باید تقریبی باشد به این صورت که مستطیل آموخته شده باید اجازه داشته باشد که برخی از نقاط داده را اشتباه برچسب گذاری کند، با برخی از نقاط دارای برچسب مثبت خارج از مستطیل یا نقاط دارای برچسب منفی در داخل آن. این به این دلیل است که یک راه حل دقیق می تواند به وجود یک نقطه داده خاص بسیار حساس باشد و خصوصی نباشد. هدف یک راه حل DP است که تعداد لازم از نقاط برچسب اشتباه را کم نگه می دارد.

ابتدا مورد تک بعدی را در نظر می گیریم (d = 1). ما به دنبال فاصله زمانی هستیم [a,b] که تمام نکات مثبت و هیچ یک از نکات منفی را پوشش نمی دهد. ما نشان می دهیم که حداکثر می توانیم این کار را انجام دهیم 2N نقاط با برچسب اشتباه ما روی نکاتی که دارای برچسب مثبت هستند تمرکز می کنیم. در اولین مرحله RSC ما آن را برش می دهیم ن کوچکترین نقاط و محاسبه یک نقطه بازه خصوصی به عنوان آ. سپس آن را برش می دهیم ن بزرگترین نقاط و محاسبه یک نقطه فاصله خصوصی به عنوان ب. راه حل [a,b] تمام نقاط دارای برچسب منفی و حداکثر برچسب های اشتباه را به درستی برچسب گذاری می کند 2N از نقاط با برچسب مثبت بنابراین، حداکثر ~2N امتیازها در مجموع به اشتباه برچسب گذاری شده اند.

تصویرسازی برای d = 1، برش می دهیم ن نقاط مثبت را ترک کرده و یک نقطه فاصله را محاسبه کنید آ، برش بزنید ن نقاط مثبت را انتخاب کنید و یک نقطه فاصله را محاسبه کنید ب.

با d > 1، روی محورها تکرار می کنیم i = 1,….,d و موارد فوق را برای من^هفتم مختصات نقاط ورودی برای به دست آوردن مقادیر آ_من ، ب_من . در هر تکرار، دو مرحله RSC را انجام می دهیم و برش می دهیم 2N نقاط با برچسب مثبت در کل برش میزنیم 2dN نقاط و تمام نقاط باقی مانده به درستی برچسب گذاری شدند. یعنی تمام نقاط با برچسب منفی خارج از فینال هستند د– مستطیل بعدی و همه نقاط دارای برچسب مثبت، به جز شاید ~2dN، داخل مستطیل دراز بکشید. توجه داشته باشید که این الگوریتم از انعطاف پذیری کامل RSC استفاده می کند، زیرا نقاط بر اساس هر محور به طور متفاوتی مرتب می شوند. از آنجایی که ما اجرا می کنیم د مراحل، تجزیه و تحلیل RSC یک عامل ریشه دوم را حذف می کند د از تعداد نقاط علامت گذاری شده اشتباه

آموزش مدل های ML با انتخاب تطبیقی ​​نمونه های آموزشی

کارایی آموزشی یا عملکرد مدل‌های ML را می‌توان با انتخاب نمونه‌های آموزشی به نحوی که به وضعیت فعلی مدل بستگی دارد، بهبود بخشید، مثلاً یادگیری برنامه درسی خودگام یا یادگیری فعال.

متداول ترین روش برای آموزش خصوصی مدل های ML DP-SGD است که در آن نویز از هر minibatch از نمونه های آموزشی به به روز رسانی گرادیان اضافه می شود. تحلیل حریم خصوصی با DP-SGD معمولاً فرض می‌کند که نمونه‌های آموزشی هستند به صورت تصادفی به مینی بچ تقسیم شده است. اما اگر یک دستور انتخاب وابسته به داده را در نمونه های آموزشی تحمیل کنیم و معیارهای انتخاب را بیشتر اصلاح کنیم ک بارها در طول آموزش، سپس تجزیه و تحلیل از طریق ترکیب DP منجر به بدتر شدن ضمانت‌های حریم خصوصی به بزرگی معادل ریشه دوم می‌شود. ک.

خوشبختانه، انتخاب نمونه با DP-SGD می‌تواند به طور طبیعی در الگوی RSC بیان شود: هر معیار انتخاب، نمونه‌های آموزشی را مجدداً ترتیب می‌دهد و هر minibatch یک برش است (که برای آن گرادیان نویز را محاسبه می‌کنیم). با تجزیه و تحلیل RSC، هیچ بدتر شدن حریم خصوصی وجود ندارد ک، که آموزش DP-SGD را با انتخاب نمونه به حوزه عملی می آورد.

نتیجه

پارادایم RSC به منظور مقابله با یک مشکل باز که در درجه اول اهمیت نظری دارد، معرفی شد، اما معلوم شد که ابزاری همه کاره با پتانسیل افزایش کارایی داده در محیط های تولید است.

قدردانی ها

کاری که در اینجا توضیح داده شد به طور مشترک با شین لیو، جلانی نلسون و تاماس سارلوس انجام شد.