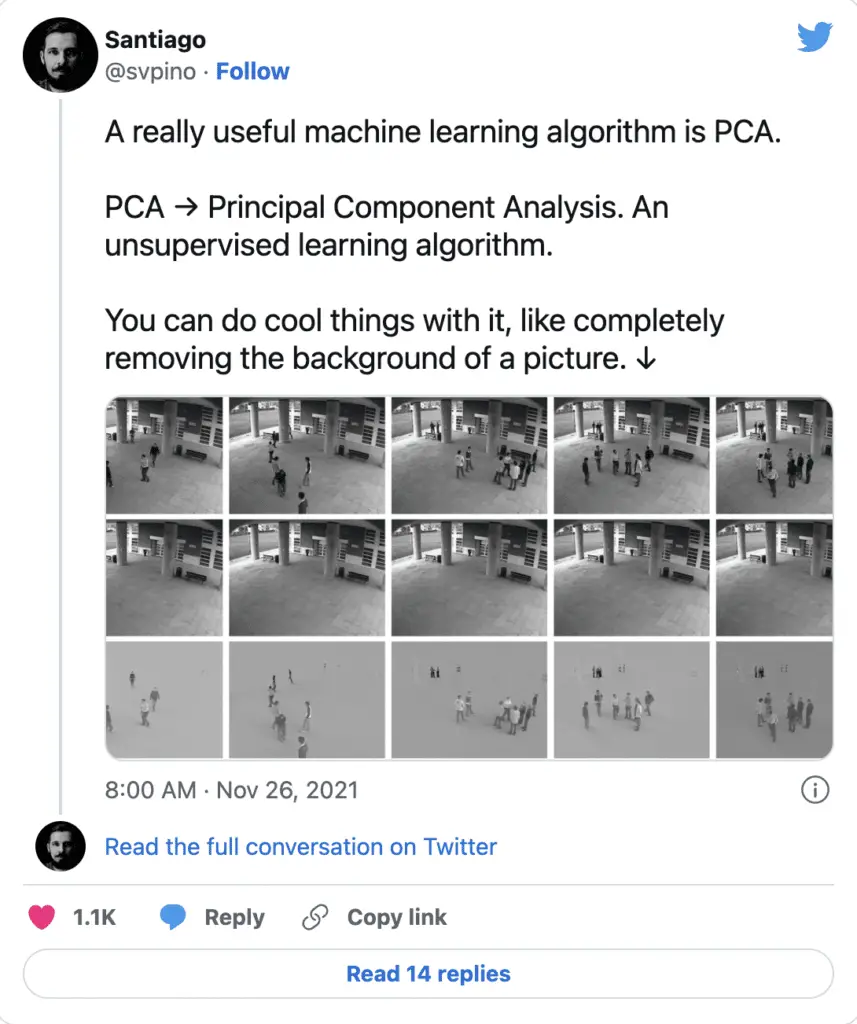
در این آموزش، با الگوریتم یادگیری ماشین PCA با استفاده از Python و Scikit-learn آشنا خواهید شد.
PCA نمونه هایی از این آموزش
تجزیه و تحلیل اجزای اصلی (PCA) چیست؟
PCA یا تجزیه و تحلیل مؤلفه اصلی، الگوریتم خطی اصلی برای کاهش ابعاد است که اغلب در یادگیری بدون نظارت استفاده می شود.
این الگوریتم ویژگیهایی را که برای ایجاد یک تقریب معتبر روی یک مجموعه داده مفید نیستند، شناسایی و کنار میگذارد.
جالب اینجاست که می تواند کارهای جالبی مانند حذف پس زمینه از یک تصویر انجام دهد.

چرا از PCA استفاده کنیم؟
با کاهش تعداد ویژگی ها، PCA می تواند کمک کند:
- خطر تطبیق بیش از حد یک مدل با ویژگی های پر سر و صدا را کاهش دهید.
- افزایش سرعت آموزش الگوریتم یادگیری ماشین
- بصری سازی داده ها را ساده تر کنید.
به عنوان مثال، مجموعه داده Iris دارای 4 ویژگی است… ترسیم یک نمودار 4 بعدی دشوار است.

با این حال، ما می توانیم از PCA برای کاهش تعداد ویژگی ها به 3 و رسم بر روی یک نمودار سه بعدی استفاده کنیم.


الگوریتم یادگیری ماشین PCA چگونه کار می کند؟
PCA بعد ذاتی یک مجموعه داده را شناسایی می کند.
به عبارت دیگر، کمترین تعداد ویژگی های مورد نیاز برای پیش بینی دقیق را شناسایی می کند.
یک مجموعه داده ممکن است ویژگی های زیادی داشته باشد، اما همه ویژگی ها برای پیش بینی ضروری نیستند.

ویژگی هایی که حفظ می شوند، آنهایی هستند که دارای واریانس قابل توجهی هستند.
- نگاشت خطی داده ها به فضایی با ابعاد کمتر به گونه ای انجام می شود که واریانس داده ها را به حداکثر می رساند.
- PCA فرض می کند که ویژگی های با واریانس کم بی ربط هستند و ویژگی های با واریانس بالا آموزنده هستند.
شروع شدن
برای این آموزش، شما همچنین باید پایتون را نصب کنید و کتابخانه های زیر را از خط فرمان یا ترمینال خود نصب کنید.
مجموعه داده Iris را بارگیری کنید
مجموعه داده Iris برای تجسم نحوه عملکرد تجزیه و تحلیل مؤلفه اصلی مفید است.
این یک مجموعه داده داخلی در Scikit-learn است و میتواند از این طریق در قالب داده پاندا بارگذاری شود.
import pandas as pd
from sklearn import datasets
iris = datasets.load_iris()
target_names = {
0:'setosa',
1:'versicolor',
2:'virginica'
}
df = pd.DataFrame(
iris.data,
columns=iris.feature_names
)
df['target'] = iris.target
df['target_names'] = df['target'].map(target_names)
چارچوب داده حاصل شامل 4 ویژگی (متغیرهای پیش بینی کننده) است که 3 گونه گل را توصیف می کند.

3 گونه گل هر کدام 50 رکورد دارند.
import matplotlib.pyplot as plt
import seaborn as sns
sns.countplot(
x='target_names',
data=df)
plt.title('Iris targets value count')
plt.show()
بارگذاری ویژگی ها و هدف به طور جداگانه
برای درک مجموعه داده Iris، آن را در یک دیتافریم بارگذاری کرده ایم. با این حال، برای اینکه آن را برای Scikit-learn قابل استفاده تر کنیم، ویژگی ها و اهداف را به عنوان آرایه های ذخیره شده در مربوطه بارگذاری می کنیم. X و y متغیرها
from sklearn import datasets
# load features and targets separately
iris = datasets.load_iris()
X = iris.data
y = iris.target

پیش پردازش داده ها
بیایید پیش پردازش داده های بسیار ابتدایی را انجام دهیم و داده ها را با استفاده از StandardScaler مقیاس بندی کنیم.
StandardScaler ویژگی ها را با حذف میانگین و مقیاس بندی به واریانس واحد استاندارد می کند تا هر ویژگی μ = 0 و σ = 1 داشته باشد.
تبدیل این:

در این مورد:

# data scaling
x_scaled = StandardScaler().fit_transform(X)
کاهش ابعاد با استفاده از PCA
ما دیدیم که مجموعه داده Iris شامل 4 ویژگی است که آن را به یک مجموعه داده 4 بعدی تبدیل می کند.
لزوماً همه ویژگی ها برای پیش بینی مفید نیستند. بنابراین، میتوانیم آن ویژگیهای پر سر و صدا را حذف کرده و مدلی سریعتر بسازیم.
PCA کاندیدای اصلی برای انجام این نوع کاهش ابعاد است.
کاری که PCA انجام می دهد تبدیل این است:
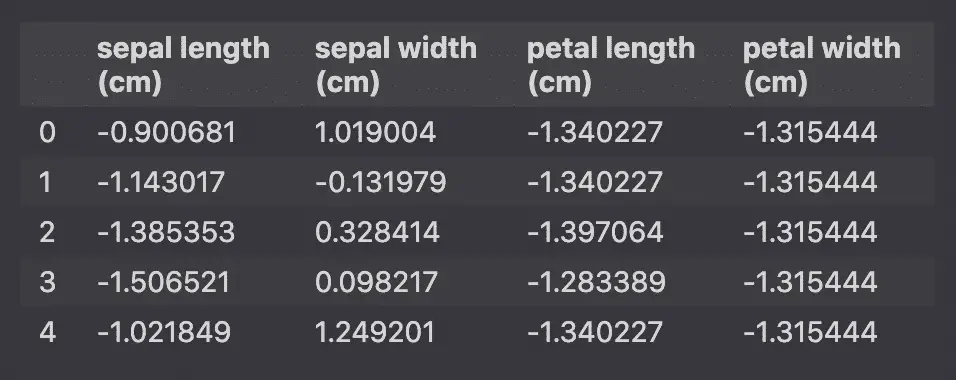
در این مورد:

را n_components آرگومان تعداد مؤلفه هایی را که می خواهیم ویژگی ها را به آنها کاهش دهیم را مشخص می کند.
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
pca_features = pca.fit_transform(x_scaled)
print('Shape before PCA: ', x_scaled.shape)
print('Shape after PCA: ', pca_features.shape)
pca_df = pd.DataFrame(
data=pca_features,
columns=['PC1', 'PC2', 'PC3'])
با کد بالا، می توانید ببینید که اعمال PCA بر تعداد ردیف ها تأثیر نمی گذارد، اما بر تعداد ستون ها تأثیر می گذارد و به جای 4، تنها 3 باقی می ماند.

نقشه اهداف به اجزای اصلی
با نگاشت نام هدف به ویژگی های PCA، چارچوب داده PCA را برای تجسم آماده می کنیم.
target_names = {
0:'setosa',
1:'versicolor',
2:'virginica'
}
pca_df['target'] = y
pca_df['target'] = pca_df['target'].map(target_names)
pca_df

هر ویژگی چقدر بر پیش بینی تأثیر می گذارد؟
را واریانس را توضیح داد، یا مقدار ویژه، در PCA واریانسی را که می توان به هر یک از اجزای اصلی نسبت داد را نشان می دهد.
آرایه ای از مقادیر است که در آن هر مقدار برابر واریانس هر جزء اصلی و طول آرایه برابر با تعداد مؤلفه های تعریف شده است. n_components.
می توان به آن دسترسی پیدا کرد .explained_variance_ نشانه گذاری.
array([2.93808505, 0.9201649 , 0.14774182])
واریانس توضیح داده شده را رسم کنید
ما می توانیم واریانس توضیح داده شده را رسم کنیم تا واریانس هر ویژگی جزء اصلی را ببینیم.
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
sns.set()
# Reduce from 4 to 3 features with PCA
pca = PCA(n_components=3)
# Fit and transform data
pca.fit_transform(x_scaled)
# Bar plot of explained_variance
plt.bar(
range(1,len(pca.explained_variance_)+1),
pca.explained_variance_
)
plt.xlabel('PCA Feature')
plt.ylabel('Explained variance')
plt.title('Feature Explained Variance')
plt.show()
نمودار خروجی نشان می دهد که ما به 3 ویژگی نیاز نداریم، بلکه فقط به 2 ویژگی نیاز داریم. واریانس ویژگی 3 واضح است که چندان قابل توجه نیست.

Scree Plot
نمودار اسکری چیزی نیست جز نمودار مقادیر ویژه (که به عنوان واریانس توضیح داده شده نیز شناخته می شود). اساساً، همان اطلاعات طرح بالا را ارائه می دهد.
اضافه کردن مجموع تجمعی واریانس توضیح داده شده می تواند به انجام تست های آرنج برای شناسایی مولفه های اصلی واریانس کم کمک کند.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.decomposition import PCA
sns.set()
# Reduce from 4 to 3 features with PCA
pca = PCA(n_components=3)
# Fit and transform data
reduced_features = pca.fit_transform(x_scaled)
# Bar plot of explained_variance
plt.bar(
range(1,len(pca.explained_variance_)+1),
pca.explained_variance_
)
plt.plot(
range(1,len(pca.explained_variance_ )+1),
np.cumsum(pca.explained_variance_),
c='red',
label='Cumulative Explained Variance')
plt.legend(loc='upper left')
plt.xlabel('Number of components')
plt.ylabel('Explained variance (eignenvalues)')
plt.title('Scree plot')
plt.show()

واریانس را به صورت بصری درک کنید
شاید واریانس برای شما گیج کننده باشد.
بیایید با ترسیم ویژگی های انتخاب شده در یک نمودار سه بعدی، یک مثال را ببینیم.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
plt.style.use('default')
# Prepare 3D graph
fig = plt.figure()
ax = plt.axes(projection='3d')
# Plot scaled features
xdata = x_scaled[:,0]
ydata = x_scaled[:,1]
zdata = x_scaled[:,2]
# Plot 3D plot
ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='viridis')
# Plot title of graph
plt.title(f'3D Scatter of Iris')
# Plot x, y, z even ticks
ticks = np.linspace(-3, 3, num=5)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
ax.set_zticks(ticks)
# Plot x, y, z labels
ax.set_xlabel('sepal_length', rotation=150)
ax.set_ylabel('sepal_width')
ax.set_zlabel('petal_length', rotation=60)
plt.show()

هنگام ترسیم یک نمودار سه بعدی، واضح تر است که واریانس کمتری در آن وجود دارد Petal length از گل زنبق نسبت به در Sepal length یا Sepal width، تقریباً یک صفحه دو بعدی مسطح در داخل نمودار سه بعدی ایجاد می کند. این نشان می دهد که بعد ذاتی داده ها به جای 4، اساساً 2 بعد است.
کاهش این 3 ویژگی به 2 نه تنها مدل را سریعتر میکند، بلکه تجسمها را بدون از دست دادن اطلاعات بسیار آموزندهتر میکند.
نمودار 2 بعدی PCA را رسم کنید
اکنون که می دانیم فقط به 2 جزء اصلی نیاز داریم، تمام مراحلی را که قبل از استفاده انجام دادیم تکرار می کنیم n_components=2.
import pandas as pd
from sklearn.decomposition import PCA
# Reduce from 4 to 2 features with PCA
pca = PCA(n_components=2)
# Fit and transform data
pca_features = pca.fit_transform(x_scaled)
# Create dataframe
pca_df = pd.DataFrame(
data=pca_features,
columns=['PC1', 'PC2'])
# map target names to PCA features
target_names = {
0:'setosa',
1:'versicolor',
2:'virginica'
}
pca_df['target'] = y
pca_df['target'] = pca_df['target'].map(target_names)
pca_df.head()

سپس با استفاده از Seaborn’s lmplot، مولفه های اصلی 2 بعدی را روی نمودار پراکندگی رسم می کنیم.
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
sns.lmplot(
x='PC1',
y='PC2',
data=pca_df,
hue='target',
fit_reg=False,
legend=True
)
plt.title('2D PCA Graph')
plt.show()

چگونه بای پلات دو بعدی بسازیم؟
Biplot ها نمودارهایی هستند که نشان می دهند:
- نمودارهای پراکنده PCA مقیاس شده
- کرت های بارگیری علاوه بر این
- بردارهایی که نشان میدهند هر ویژگی چقدر بر مؤلفه اصلی تأثیر میگذارد.
در حال بارگذاری قطعه ها
نمودار بارگذاری بردارهایی را نشان می دهد که از مبدا تا بارگذاری هر ویژگی شروع می شوند.
بارگذاری ها (یا وزن ها) ضرایب همبستگی بین ویژگی های اصلی و اجزای اصلی هستند.
آنها عناصر بردار ویژه را نشان می دهند.
بارهای مربعی اجزای اصلی همیشه برابر با 1 است.
با استفاده از بارگیری ها قابل دسترسی است pca.components_.
با الهام از Renesh Bedre، من یک طرح بارگذاری ایجاد خواهم کرد تا به درک آنها کمک کنم.
ابتدا ضرایب همبستگی هر ویژگی / جزء اصلی را رسم می کنیم.
ایجاد چارچوب داده ضرایب همبستگی
برای درک اینکه چگونه هر ویژگی بر هر مؤلفه اصلی (PC) تأثیر می گذارد، ارتباط بین ویژگی ها و مؤلفه های اصلی ایجاد شده با PCA را نشان خواهیم داد.
# Principal components correlation coefficients
loadings = pca.components_
# Number of features before PCA
n_features = pca.n_features_
# Feature names before PCA
feature_names = iris.feature_names
# PC names
pc_list = [f'PC{i}' for i in list(range(1, n_features + 1))]
# Match PC names to loadings
pc_loadings = dict(zip(pc_list, loadings))
# Matrix of corr coefs between feature names and PCs
loadings_df = pd.DataFrame.from_dict(pc_loadings)
loadings_df['feature_names'] = feature_names
loadings_df = loadings_df.set_index('feature_names')
loadings_df
نتیجه یک چارچوب داده با بارگذاری ها (ضرایب همبستگی) است.

چگونه یک نمودار بارگذاری دو بعدی بسازیم
نمودار بارگذاری کمک می کند تا بفهمیم کدام ویژگی بر کدام مؤلفه اصلی و چقدر تأثیر می گذارد.
ابتدا ضرایب همبستگی (بارگذاری) هر ویژگی را رسم می کنیم.
import matplotlib.pyplot as plt
import numpy as np
# Get the loadings of x and y axes
xs = loadings[0]
ys = loadings[1]
# Plot the loadings on a scatterplot
for i, varnames in enumerate(feature_names):
plt.scatter(xs[i], ys[i], s=200)
plt.text(xs[i], ys[i], varnames)
# Define the axes
xticks = np.linspace(-0.8, 0.8, num=5)
yticks = np.linspace(-0.8, 0.8, num=5)
plt.xticks(xticks)
plt.yticks(yticks)
plt.xlabel('PC1')
plt.ylabel('PC2')
# Show plot
plt.title('2D Loading plot')
plt.show()

سپس جهت همبستگی را با افزودن فلش هایی از مبدا (0، 0) به هر یک از ضرایب رسم می کنیم.
import matplotlib.pyplot as plt
import numpy as np
# Get the loadings of x and y axes
xs = loadings[0]
ys = loadings[1]
# Plot the loadings on a scatterplot
for i, varnames in enumerate(feature_names):
plt.scatter(xs[i], ys[i], s=200)
plt.arrow(
0, 0, # coordinates of arrow base
xs[i], # length of the arrow along x
ys[i], # length of the arrow along y
color='r',
head_width=0.01
)
plt.text(xs[i], ys[i], varnames)
# Define the axes
xticks = np.linspace(-0.8, 0.8, num=5)
yticks = np.linspace(-0.8, 0.8, num=5)
plt.xticks(xticks)
plt.yticks(yticks)
plt.xlabel('PC1')
plt.ylabel('PC2')
# Show plot
plt.title('2D Loading plot with vectors')
plt.show()

داده های PCA را مقیاس کنید
ما نمودار PCA را دوباره مقیاس می کنیم تا آن را در برابر نمودارهای بارگذاری رسم کنیم.
من برخی از کدهای زیر را از آموزش فوق العاده Prasad Ostwal در مورد PCA قرض گرفته ام.
pca_df_scaled = pca_df.copy()
scaler_df = pca_df[['PC1', 'PC2']]
scaler = 1 / (scaler_df.max() - scaler_df.min())
for index in scaler.index:
pca_df_scaled[index] *= scaler[index]
pca_df_scaled

طرح Scatterplot و Loading را در یک Biplot ترکیب کنید
با استفاده از نمودارهای بارگذاری و نمودارهای مقیاس شده، اکنون می توانیم ضرایب همبستگی را در برابر نمودار پراکندگی PCA در همان نمودار نشان دهیم.
# 2D
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
xs = loadings[0]
ys = loadings[1]
sns.lmplot(
x='PC1',
y='PC2',
data=pca_df_scaled,
fit_reg=False,
)
for i, varnames in enumerate(feature_names):
plt.scatter(xs[i], ys[i], s=200)
plt.arrow(
0, 0, # coordinates of arrow base
xs[i], # length of the arrow along x
ys[i], # length of the arrow along y
color='r',
head_width=0.01
)
plt.text(xs[i], ys[i], varnames)
xticks = np.linspace(-0.8, 0.8, num=5)
yticks = np.linspace(-0.8, 0.8, num=5)
plt.xticks(xticks)
plt.yticks(yticks)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.title('2D Biplot')
plt.show()

چگونه بای پلات سه بعدی بسازیم؟
بای پلات سه بعدی تمام مراحل بالا را با استفاده از 3 جزء به جای 2 ترکیب می کند.
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from mpl_toolkits.mplot3d import Axes3D
plt.style.use('default')
pca = PCA(n_components=3)
# Fit and transform data
pca_features = pca.fit_transform(x_scaled)
# Create dataframe
pca_df = pd.DataFrame(
data=pca_features,
columns=['PC1', 'PC2', 'PC3'])
# map target names to PCA features
target_names = {
0:'setosa',
1:'versicolor',
2:'virginica'
}
# Apply the targett names
pca_df['target'] = iris.target
pca_df['target'] = pca_df['target'].map(target_names)
# Create the scaled PCA dataframe
pca_df_scaled = pca_df.copy()
scaler_df = pca_df[['PC1', 'PC2', 'PC3']]
scaler = 1 / (scaler_df.max() - scaler_df.min())
for index in scaler.index:
pca_df_scaled[index] *= scaler[index]
# Initialize the 3D graph
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Define scaled features as arrays
xdata = pca_df_scaled['PC1']
ydata = pca_df_scaled['PC2']
zdata = pca_df_scaled['PC3']
# Plot 3D scatterplot of PCA
ax.scatter3D(
xdata,
ydata,
zdata,
c=zdata,
cmap='Greens',
alpha=0.5)
# Define the x, y, z variables
loadings = pca.components_
xs = loadings[0]
ys = loadings[1]
zs = loadings[2]
# Plot the loadings
for i, varnames in enumerate(feature_names):
ax.scatter(xs[i], ys[i], zs[i], s=200)
ax.text(
xs[i] + 0.1,
ys[i] + 0.1,
zs[i] + 0.1,
varnames)
# Plot the arrows
x_arr = np.zeros(len(loadings[0]))
y_arr = z_arr = x_arr
ax.quiver(x_arr, y_arr, z_arr, xs, ys, zs)
# Plot title of graph
plt.title(f'3D Biplot of Iris')
# Plot x, y, z labels
ax.set_xlabel('Principal component 1', rotation=150)
ax.set_ylabel('Principal component 2')
ax.set_zlabel('Principal component 3', rotation=60)
plt.show()

مقالات با استفاده از PCA
اشاره ویژه به پست های باورنکردنی در PCA
نحوه ساخت PCA در پایتون
برای انجام کاهش ابعاد با استفاده از تجزیه و تحلیل مؤلفه اصلی Scikit-learn (PCA) و پایتون:
- بارگذاری داده ها
میتوانید هر مجموعه داده برچسبگذاری شدهای را که میخواهید روی آن پیشبینی کنید، بارگیری کنید. به عنوان مثال، می توانید استفاده کنید
datasets.load_iris()روی مجموعه داده Iris برای تمرین. - مجموعه داده را کاوش کنید
از توابع پانداهای پایتون مانند
df.describe()وdf.isnull().sum()برای پیدا کردن نحوه پردازش داده های شما در آموزش قبلی - پیش پردازش داده ها
مقادیر گمشده یا ناخواسته را از مجموعه داده خود رها کنید، پر کنید یا نسبت دهید تا مطمئن شوید که خطا یا سوگیری در داده های خود وارد نمی کنید. از اسکلرن استفاده کنید
StandardScalerبرای استاندارد کردن ویژگی ها - کاهش ابعاد PCA را انجام دهید
نمونه سازی با sklearn’s
decomposition.PCAو استفاده کنیدfit_transform()روش کاهش تعداد ویژگی ها به مجموعه تعریف شدهn_components. - نمودار 2 بعدی PCA را رسم کنید
از sns.lmplot() seaborn برای رسم نمودار 2 بعدی PCA و تجسم داده های خود استفاده کنید.
تعاریف PCA و یادگیری ماشین
| تجزیه و تحلیل مؤلفه های اصلی | الگوریتم خطی برای کاهش ابعاد |
| کتابخانه PCA Python | sklearn.decomposition.PCA |
| PCA را در پایتون ترسیم کنید | Searborn lmplot() را می توان استفاده کرد |
| استفاده از PCA | سرعت و سادگی |
روش های PCA
در اینجا جدولی وجود دارد که تمام روش هایی را که می توان روی شی PCA اعمال کرد فهرست می کند.
| مناسب() | مدل را با X مناسب کنید. |
| fit_transform() | مدل را با X مطابقت دهید و کاهش ابعاد را روی X اعمال کنید. |
| get_covariance() | محاسبه کوواریانس داده ها با مدل مولد. |
| get_feature_names_out() | دریافت نام ویژگی های خروجی برای تبدیل. |
| get_params() | پارامترهای این برآوردگر را دریافت کنید. |
| get_precision() | محاسبه ماتریس دقت داده ها با مدل مولد. |
| inverse_transform() | داده ها را به فضای اصلی خود تبدیل کنید. |
| نمره() | میانگین احتمال ورود به سیستم همه نمونه ها را برگردانید. |
| score_samples() | احتمال گزارش هر نمونه را برگردانید. |
| set_params() | پارامترهای این برآوردگر را تنظیم کنید. |
| تبدیل() | کاهش ابعاد را به X اعمال کنید. |
نتیجه
تبریک می گویم، شما اکنون یکی از مهم ترین تکنیک های کاهش ابعاد را یاد گرفته اید.
با تجزیه و تحلیل اجزای اصلی (PCA) شما مدل های یادگیری ماشین را بهینه کرده اید و تجسم های روشنگرتری ایجاد کرده اید.
شما همچنین یاد گرفتید که چگونه رابطه بین هر ویژگی و جزء اصلی را با ایجاد نمودارهای بارگذاری دوبعدی و سه بعدی و بای پلات ها درک کنید.

استراتژیست سئو در Tripadvisor، Seek سابق (ملبورن، استرالیا). متخصص در سئو فنی. در تلاش برای سئوی برنامهریزی شده برای سازمانهای بزرگ از طریق استفاده از پایتون، R و یادگیری ماشین.